题目内容
对定义在实数集R上的函数f1(x),f2(x),令F(x)=f1(x)+f2(x),已知对任意不同的实数x1,x2,|f1(x1)-f1(x2)|>|f2(x1)-f2(x2)|.
(1)若y=f1(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(2)若y=f2(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(3)求函数f(x)=x2+
(x>0)的单调区间.
(1)若y=f1(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(2)若y=f2(x)是区间D上的增函数,能否确定y=F(x)是区间D上的增函数?若能够确定,说明理由;若不能,请举例说明;
(3)求函数f(x)=x2+
| 1 | 4x |
分析:(1)设x1<x2由y=f1(x)是区间D上的增函数可得f1(x1)<f1(x2),①若f2(x)为单调递增或常函数,则y=F(x)是区间D上的增函数;②若函数f2(x1)>f2(x2),则由|f1(x1)-f1(x2)|>|f2(x1)-f2(x2)|可得,-f1(x1)+f1(x2)|>f2(x1)-f2(x2),从而可判断
(2)例如函数f1(x)=-3x,f2(x)=2x,则F(x)=2x-3x不是单调递增函数
(3)对函数求导可得f′(x)=2x-
=
结合x>0,分别求f′(x)≥0,f′(x)<0的x的范围,从而可求函数的单调区间
(2)例如函数f1(x)=-3x,f2(x)=2x,则F(x)=2x-3x不是单调递增函数
(3)对函数求导可得f′(x)=2x-
| 1 |
| 4x2 |
| 8x3-1 |
| 4x2 |
解答:解:(1)设x1<x2由y=f1(x)是区间D上的增函数可得f1(x1)<f1(x2)
①若f2(x)为单调递增或常函数,则y=F(x)是区间D上的增函数
②若函数f2(x1)>f2(x2),则由|f1(x1)-f1(x2)|>|f2(x1)-f2(x2)|可得,-f1(x1)+f1(x2)|>f2(x1)-f2(x2)
∴f1(x1)+f2(x1)<f1(x2)+f2(x2)即F(x1)<F(x2)
综上可得函数F(X)为单调递增的函数
(2)例如函数f1(x)=-3x,f2(x)=2x,则F(x)=2x-3x不是单调递增函数
(3)f′(x)=2x-
=
∵x>0由f′(x)≥0可得x≥
,f′(x)<0可得0<x<
函数f(x)的单调增区间是[
,+∞),单调减区间是(0,
)
①若f2(x)为单调递增或常函数,则y=F(x)是区间D上的增函数
②若函数f2(x1)>f2(x2),则由|f1(x1)-f1(x2)|>|f2(x1)-f2(x2)|可得,-f1(x1)+f1(x2)|>f2(x1)-f2(x2)
∴f1(x1)+f2(x1)<f1(x2)+f2(x2)即F(x1)<F(x2)
综上可得函数F(X)为单调递增的函数
(2)例如函数f1(x)=-3x,f2(x)=2x,则F(x)=2x-3x不是单调递增函数
(3)f′(x)=2x-
| 1 |
| 4x2 |
| 8x3-1 |
| 4x2 |
∵x>0由f′(x)≥0可得x≥
| 1 |
| 2 |
| 1 |
| 2 |
函数f(x)的单调增区间是[
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了利用函数的单调性的定义判断函数的单调性及利用导数求解函数的单调区间,解题的关键是要灵活利用函数单调性的知识.

练习册系列答案
相关题目
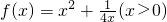 的单调区间.
的单调区间.