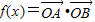题目内容
已知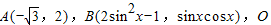 为坐标原点,
为坐标原点,
(1)求f(x)的值域与最小正周期;
(2)试描述函数f(x)的图象是由函数y=sinx的图象经过怎样的变换得到?
【答案】分析:(1)利用两个向量的数量积公式求出f(x)=2sin(2x+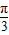 ),由此求得f(x)的值域与最小正周期.
),由此求得f(x)的值域与最小正周期.
(2)根据函数y=Asin(ωx+∅)的图象变换规律,得出结论.
解答:解:(1)由题意可得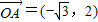 ,
,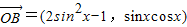 ,…(1分)
,…(1分)
∴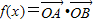 =
=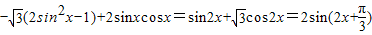 ,…5
,…5
故函数的值域为[-2,2],周期为T=π.…(7分)
(2)把函数y=sinx的图象的横坐标变为原来的一半,可得函数y=sin2x的图象,再向左平移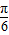 个单位可得y=sin(2x+
个单位可得y=sin(2x+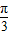 )的图象,
)的图象,
再把各点的纵坐标变为原来的2倍,即可得到函数f(x)=2sin(2x+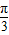 )的图象.
)的图象.
点评:本题主要考查两个向量的数量积公式的应用,正弦函数的值域和周期性,函数y=Asin(ωx+∅)的图象变换规律,属于基础题.
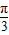 ),由此求得f(x)的值域与最小正周期.
),由此求得f(x)的值域与最小正周期.(2)根据函数y=Asin(ωx+∅)的图象变换规律,得出结论.
解答:解:(1)由题意可得
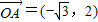 ,
,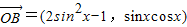 ,…(1分)
,…(1分)∴
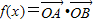 =
=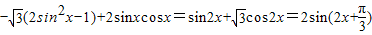 ,…5
,…5故函数的值域为[-2,2],周期为T=π.…(7分)
(2)把函数y=sinx的图象的横坐标变为原来的一半,可得函数y=sin2x的图象,再向左平移
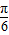 个单位可得y=sin(2x+
个单位可得y=sin(2x+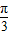 )的图象,
)的图象,再把各点的纵坐标变为原来的2倍,即可得到函数f(x)=2sin(2x+
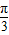 )的图象.
)的图象.点评:本题主要考查两个向量的数量积公式的应用,正弦函数的值域和周期性,函数y=Asin(ωx+∅)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 为坐标原点,向量
为坐标原点,向量 ,
, ,点
,点 满足
满足 .
. ,讨论函数
,讨论函数 的单调性,并求其值域;
的单调性,并求其值域; 三点共线,求
三点共线,求 的值.
的值.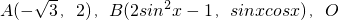 为坐标原点,
为坐标原点,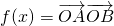
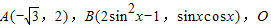 为坐标原点,
为坐标原点,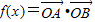
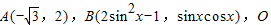 为坐标原点,
为坐标原点,