题目内容
给出下列结论,其中不正确的是( )
分析:利用命题的否定可判断A;
先解出x2<4的解,再判断两命题的关系可判断B;
我们知道:“若p,则q”的否命题是“若¬p,则¬q”,据此可求出其否命题.可判断C;
利用复合命题的真值表可判断D.
先解出x2<4的解,再判断两命题的关系可判断B;
我们知道:“若p,则q”的否命题是“若¬p,则¬q”,据此可求出其否命题.可判断C;
利用复合命题的真值表可判断D.
解答:解:A、由命题的否定知,若命题p:?x0∈R,x02+x0+1<0,则¬p:?x0∈R,x02+x0+1≥0,故A为真命题,
B、由x2<4,得:-2<x<2,
则由-2<x<2可以推出x<2,
故“x2<4”是“x<2”的充分不必要条件,故B为真命题;
C、根据:“若p,则q”的否命题是“若¬p,则¬q”,
所以命题“若一个数是负数,则它的平方是正数”的否命题是“若一个数不是负数,则它的平方不是正数”.
故C正确;
D、命题p是“甲获奖”,则¬p是“甲没有获奖”,
q是“乙获奖”,则¬q是“乙没有获奖”,
命题“至少有一人没有获奖”包括:
“甲没获奖,乙获奖”或“甲获奖,乙没有获奖”或“甲没有获奖,乙没有获奖”三种情况.
所以命题“至少有一人没有获奖”可表示为(¬p)∨(¬q).故D为假命题.
故答案为:D.
B、由x2<4,得:-2<x<2,
则由-2<x<2可以推出x<2,
故“x2<4”是“x<2”的充分不必要条件,故B为真命题;
C、根据:“若p,则q”的否命题是“若¬p,则¬q”,
所以命题“若一个数是负数,则它的平方是正数”的否命题是“若一个数不是负数,则它的平方不是正数”.
故C正确;
D、命题p是“甲获奖”,则¬p是“甲没有获奖”,
q是“乙获奖”,则¬q是“乙没有获奖”,
命题“至少有一人没有获奖”包括:
“甲没获奖,乙获奖”或“甲获奖,乙没有获奖”或“甲没有获奖,乙没有获奖”三种情况.
所以命题“至少有一人没有获奖”可表示为(¬p)∨(¬q).故D为假命题.
故答案为:D.
点评:本题考查命题的真假判断与应用,掌握命题之间的等价关系及复合命题的真值表及命题的否定是关键,属于基础题.

练习册系列答案
相关题目
 )|的最小正周期是
)|的最小正周期是 ;
;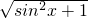 )有无奇偶性不能确定.
)有无奇偶性不能确定.