题目内容
1.定义域为R的函数f(x)对任意x都有f(x)=f(4-x),且其导函数f′(x)满足(x-2)f′(x)>0,则当2<m<4时,有( )| A. | f(2)>f(2m)>f(log2m) | B. | f(log2m)>f(2m)>f(2) | C. | f(2m)>f(log2m)>f(2) | D. | f(2m)>>f(2)>f(log2m) |
分析 先根据条件求出函数的对称轴,再求出函数的单调区间,然后判定2、log2m、2m的大小关系,根据单调性比较f(2)、f(log2m)、f(2m)的大小即可.
解答 解:∵函数f(x)对任意x都有f(x)=f(4-x),
∴函数f(x)的对称轴为x=2
∵导函数f′(x)满足 (x-2)f′(x)>0,∴函数f(x)在(2,+∞)上单调递增,(-∞,2)上单调递减
∵2<m<4
∴2<log2m<2m
∴f(2m)>f(log2m)>f(2).
故选:C.
点评 本题主要考查了导数的运算,以及奇偶函数图象的对称性和比较大小,同时考查了数形结合的思想,该题有一定的思维量,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.在△ABC中,已知(a2+b2-c2)2=2(ab)2,则C等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 45°或135° |
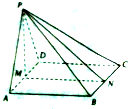 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.