题目内容
设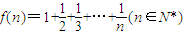 ,是否存在g(n),使得等式f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)总成立?若存在,请写出g(n)通项公式(不必说明理由);若不存在,说明理由. .
,是否存在g(n),使得等式f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)总成立?若存在,请写出g(n)通项公式(不必说明理由);若不存在,说明理由. .
【答案】分析:先将f(1)+f(2)+f(3)+…+f(n)用f(n)表示,然后代入f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)可求出g(n)的解析式.
解答:解:f(1)=1
f(2)=1+
f(3)=1+ +
+
…
f(n)=1+ +
+ +…
+…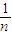
所以f(1)+f(2)+f(3)+…+f(n)
=n×1+ (n-1)+
(n-1)+ (n-2)…
(n-2)…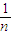 [n-(n-1)]
[n-(n-1)]
=n[1+ +
+ +…
+…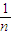 ]-[
]-[ +
+ +
+ …
…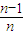 ]
]
=nf(n)-[1- +1-
+1- +1-
+1- …1-
…1-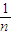 ]
]
=nf(n)-[(n-1)-f(n)+1]
=(n+1)f(n)-n
因为f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)
所以(n+1)f(n)=ng(n)f(n)
所以g(n)=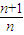
故答案为:存在,通项公式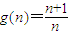
点评:本题主要考查了数列的求和,以及存在性问题,同时考查了计算能力和转化能力,属于中档题.
解答:解:f(1)=1
f(2)=1+

f(3)=1+
 +
+
…
f(n)=1+
 +
+ +…
+…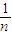
所以f(1)+f(2)+f(3)+…+f(n)
=n×1+
 (n-1)+
(n-1)+ (n-2)…
(n-2)…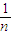 [n-(n-1)]
[n-(n-1)]=n[1+
 +
+ +…
+…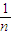 ]-[
]-[ +
+ +
+ …
…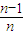 ]
]=nf(n)-[1-
 +1-
+1- +1-
+1- …1-
…1-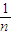 ]
]=nf(n)-[(n-1)-f(n)+1]
=(n+1)f(n)-n
因为f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)
所以(n+1)f(n)=ng(n)f(n)
所以g(n)=
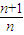
故答案为:存在,通项公式
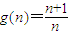
点评:本题主要考查了数列的求和,以及存在性问题,同时考查了计算能力和转化能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
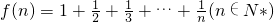 ,是否存在g(n),使得等式f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)总成立?若存在,请写出g(n)通项公式(不必说明理由);若不存在,说明理由.________.
,是否存在g(n),使得等式f(1)+f(2)+f(3)+…+f(n)+n=ng(n)f(n)总成立?若存在,请写出g(n)通项公式(不必说明理由);若不存在,说明理由.________. ,是否存在g(n),使等式f(1)+f(2)+…+f(n-1)=g(n)f(n)-1
,是否存在g(n),使等式f(1)+f(2)+…+f(n-1)=g(n)f(n)-1