题目内容
某厂拟生产甲、乙两种适销产品,每件销售收入分别为0.3万元、0.2万元.甲、乙两种产品都需在A、B两种设备上加工,在每台A、B设备上加工1件甲产品设备所需工时分别为1 h、2 h,加工1件乙产品设备所需工时分别为2 h、1 h,A、B两种设备每月有效使用台时数分别为400 h、500 h.则月销售收入的最大值为
(A)50万元 (B)70万元 (C)80万元 (D)100万元
(A)50万元 (B)70万元 (C)80万元 (D)100万元
C
专题:应用题;不等式的解法及应用.
分析:先设甲、乙两种产品月产量分别为x、y件,写出约束条件、目标函数,欲求生产收入最大值,即求可行域中的最优解,将目标函数看成是一条直线,分析目标函数Z与直线截距的关系,进而求出最优解.
解答:

解:设甲、乙两种产品月的产量分别为x,y件,
约束条件是
|
由约束条件画出可行域,如图所示的阴影部分
由z=0.3x+0.2y可得5z为直线z=0.3x+0.2y在y轴上的截距,截距最大时z最大.
结合图象可知,z=0.3x+0.2y在A处取得最大值
由
|
故选C

练习册系列答案
相关题目
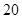 的样本数据,分组后组距与频数如下表:
的样本数据,分组后组距与频数如下表:





 上的频率为__________________.
上的频率为__________________.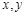 的值
的值
 的样本,如果抽出的样本中小叶榕树苗有80棵,那么此样本的容量
的样本,如果抽出的样本中小叶榕树苗有80棵,那么此样本的容量 。
。