题目内容

（2013•成都模拟）若实数x，y满足条件
x+y≥0
x-y+3≥0
0≤x≤3
，则z=2x-y的最大值为（　　）
分析：画出不等式表示的平面区域，z=2x-y的几何意义是直线y=2x-z的纵截距的相反数，根据图形可得结论．
解答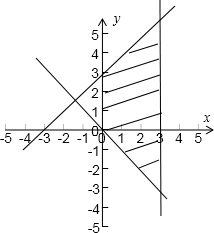：解：画出不等式表示的平面区域
z=2x-y的几何意义是直线y=2x-z的纵截距的相反数，
由
x=3
x+y=0
可得交点坐标为（3，-3），根据图形可知在点（3，-3）处，z=2x-y取得最大值，最大值为9
故选A．
点评：本题考查线性规划知识的运用，解题的关键是正确画出不等式组表示的平面区域，明确目标函数的几何意义．
练习册系列答案
相关题目
（2013•成都模拟）函数f（x）的定义域为D，若存在闭区间[m，n]⊆D，使得函数f（x）满足：①f（x）在[m，n]上是单调函数；②f（x）在[m，n]上的值域为[2m，2n]，则称区间[m，n]为y=f（x）的“倍值区间”．下列函数中存在“倍值区间”的有
①③④
①③④
（填上所有正确的序号）
①f（x）=x2（x≥0）；②f（x）=ex（x∈R）；③f（x）=
4x
x2+1
(x≥0)；④f（x）=loga(ax-
1
8
)(a＞0，a≠1)．
（2013•成都模拟）某大学对1000名学生的自主招生水平测试成绩进行统计，得到样本频率分布直方图（如图），则这1000名学生在该次自主招生水平测试中不低于70分的学生数是
600
600
．
（2013•成都模拟）已知向量
.
m
=（
3
sin
x
4
，1），
.
n
=（cos
x
4
，cos2
x
4
），f（x）=
.
m
•
.
n
．
（1）若f（x）=1，求cos（x+
π
3
）的值；
（2）在△ABC中，角A，B，C的对边分别是a，b，c且满足acosC+
1
2
c=b，求函数f（B）的取值范围．
（2013•成都模拟）设函数f（x）=
-x，x≤0
x2，x＞0
，若f（α）=4，则实数α为
-4或2
-4或2
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网