Question

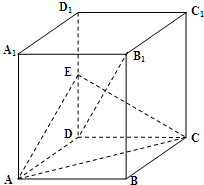如图，在正四棱柱ABCD-A₁B₁C₁D₁中，AA1=

2

，AB=1，E是DD₁的中点．
（1）求证：AC⊥B₁D；
（2）求二面角E-AC-B的大小．

Answer 1

分析：（1）法一：几何法．要证明线线垂直可利用线线垂直的判定定理．
    法二：空间向量．建立空间直角坐标系求出点A，C，D，B₁然后求出

AC

 ，

DB1

利用向量

AC

•

DB1

=0?AC⊥B₁D．
（2）法一：几何法．要求二面角的大小须先利用三垂线定理做出二面角的平面角然后在所做的三角形中求角的大小．
    法二：空间向量．建立空间直角坐标系然后利用cosθ=

a • b

| a || b |

求出θ的大小（其中

a

，

b

分别为两个平面的法向量而θ与二面角的平面角相等或互补）．

解答：（本小题满分14分）
解法一：
（1）证明：连接BD．
∵ABCD-A₁B₁C₁D₁是正四棱柱，∴B₁B⊥平面ABCD，
∴BD是B₁D在平面ABCD上的射影，…．（2分）
∵底面ABCD是正方形，∴AC⊥BD，…．（4分）
根据三垂线定理∴AC⊥B₁D．…..（6分）
（2）解：设AC∩BD=F，连接EF．∵DE⊥平面ABCD，且AC⊥BD，…（7分）
根据三垂线定理得 AC⊥FE，又AC⊥FB，∴∠EFB是二面角E-AC-B的平面角．…..（9分）
在Rt△EDF中，由DE=DF=

2

2

，得∠EFD=45°．…..（12分）
∴∠EFB=180°-45°=135°，…（13分）
即二面角E-AC-B的大小是135°．…..（14分）

解法二：∵ABCD-A₁B₁C₁D₁是正四棱柱，∴DA、DC、DD₁两两互相垂直
如图，以D为原点，直线DA，DC，DD₁分别为x轴，y轴，z轴，建立空间直角坐标系．…．（1分）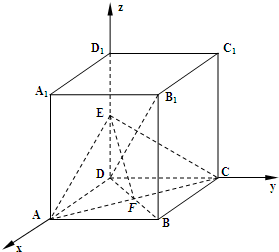

D(0，0，0)，A(1，0，0)，B(1，1，0)， C(0，1，0)，B1(1，1， 2 )

…..（3分）
（1）证明：
∵

AC

=(-1，1，0)，

DB1

=(1，1，

2

)…．（4分）
∴

AC

•

DB1

=0，∴AC⊥B₁D．…..（6分）

（2）解：
连接BD，设AC∩BD=F，连接EF．
∵DE⊥平面ABCD，且AC⊥BD∴AC⊥FE，AC⊥FB…（8分）
∴∠EFB是二面角E-AC-B的平面角．…..（9分）
∵底面ABCD是正方形
∴F(

1

2

，

1

2

，0)，∴

FB

=(

1

2

，

1

2

，0)，

FE

=(-

1

2

，-

1

2

，

2

2

)，．…．（11分）
…..（13分）
∴cos＜

FB

，

FE

＞=

FB • FE

| FB || FE |

=-

2

2

…（13分）

∴二面角E-AC-B的大小是135°．…..（14分）

点评：本题主要考查了线线垂直的证明和二面角的平面角以及求法．在解题过程中解法（1）采用了几何法证明和求解而采用此法的关键是要对面面垂直的判定定理理解透彻和如何利用几何法做出二面角的平面角的做法要熟悉（即过其中一个面内的一点向另一个面作垂线（如本题中的ED）只要垂线找到了再利用三垂线定理即可作出二面角的平面角．而解法（2）则利用了向量的方法．向量法思路简单但计算较繁琐：首先需建立空间直角坐标系然后需求点的坐标和所需向量然后代入公式求解比如本题中

AC

•

DB1

=0?AC⊥B₁D和cos＜

FB

，

FE

＞=

FB • FE

| FB || FE |

．