题目内容
有A、B两个口袋,A袋中有6张卡片,其中1张写0,2张写1,3张写有2;B袋中7张卡片,其中4张写有0,1张写有1,2张写有2,从A袋中取1张卡片,B袋中取2张卡片,共3张卡片,求:(1)取出的3张卡片都写0的概率;(2)取出的3张卡片数字之积是4的概率;
(3)取出的3张卡片数字之积的数字期望.
(1)解:(I)由题意知本题是一个古典概型,
记“取出的3张卡片都标有数字0”为事件A.
∵试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法.
而A事件表示的事件是A袋中任意取1张卡片是0,B袋中任意取2张卡都是0共有C11C42种取法,
∴ ;
;
(2)(Ⅱ)由题意知本题是一个古典概型,
记“取出的3张卡片数字之积是4”为事件B.
∵试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法.
而取出的3张卡片数字之积是4包括A袋中取得1,B袋中取得两个2;
A袋里取得一个2,B袋中取得一个2一个1,共有C21C22+C31C11C21种方法,
∴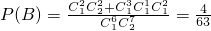 ;
;
(3)ξ的可能取值为0,2,4,8
 ,
,
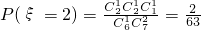 ;
;
 ;
;
ξ的概率分布列为:
 .
.
分析:(1)由题意知本题是一个古典概型,试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法.而满足条件事件表示的事件是A袋中任意取1张卡片是0,B袋中任意取2张卡都是0共有C11C42种取法,
(2)由题意知本题是一个古典概型,试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法,而取出的3张卡片数字之积是4包括A袋中取得1,B袋中取得两个2;A袋里取得一个2,B袋中取得一个2一个1,共有C21C22+C31C11C21种方法.
(3)ξ的可能取值为0,2,4,8,可先求ξ为2,4,8使得概率,ξ=0的概率用分布列的性质求解.
点评:高中必修中学习了几何概型和古典概型两种概率问题,解题时,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数,同时考查抽象概括能力和运用所学知识分析问题解决问题的能力,属中档题.
记“取出的3张卡片都标有数字0”为事件A.
∵试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法.
而A事件表示的事件是A袋中任意取1张卡片是0,B袋中任意取2张卡都是0共有C11C42种取法,
∴
 ;
;(2)(Ⅱ)由题意知本题是一个古典概型,
记“取出的3张卡片数字之积是4”为事件B.
∵试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法.
而取出的3张卡片数字之积是4包括A袋中取得1,B袋中取得两个2;
A袋里取得一个2,B袋中取得一个2一个1,共有C21C22+C31C11C21种方法,
∴
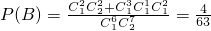 ;
;(3)ξ的可能取值为0,2,4,8
 ,
,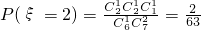 ;
; ;
;ξ的概率分布列为:
| ξ | 0 | 2 | 4 | 8 |
| P | 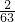 | 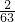 |  | 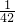 |
 .
.分析:(1)由题意知本题是一个古典概型,试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法.而满足条件事件表示的事件是A袋中任意取1张卡片是0,B袋中任意取2张卡都是0共有C11C42种取法,
(2)由题意知本题是一个古典概型,试验发生时包含的所有事件是从A袋中任意取1张卡片,B袋中任意取2张卡片共取3张卡片共有C61C72种取法,而取出的3张卡片数字之积是4包括A袋中取得1,B袋中取得两个2;A袋里取得一个2,B袋中取得一个2一个1,共有C21C22+C31C11C21种方法.
(3)ξ的可能取值为0,2,4,8,可先求ξ为2,4,8使得概率,ξ=0的概率用分布列的性质求解.
点评:高中必修中学习了几何概型和古典概型两种概率问题,解题时,先要判断该概率模型是不是古典概型,再要找出随机事件A包含的基本事件的个数和试验中基本事件的总数,同时考查抽象概括能力和运用所学知识分析问题解决问题的能力,属中档题.

练习册系列答案
相关题目
有A、B两个口袋,A袋装有4个白球,2个黑球;B袋装有3个白球,4个黑球,从A袋、B袋各取1个球交换之后,则A袋中装有4个白球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|