题目内容
合肥一中为了了解学校食堂的服务质量情况,对在校就餐的1400名学生按5%的比例进行问卷调查,把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如下表所示(服务满意度为x,价格满意度为y).
(I)作出“价格满意度”的频率分布直方图;

(II)求“服务满意度”为3时的5个“价格满意度”数据的标准差;(
≈2.1)
(III)为改进食堂服务质量,现从x<3,y<3的五人中抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.
人数 y x |
价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服 务 满 意 度 |
1 | 1 | 1 | 2 | 2 | 0 |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 0 | 1 | 2 | 3 | 1 | |

(II)求“服务满意度”为3时的5个“价格满意度”数据的标准差;(
| 4.4 |
(III)为改进食堂服务质量,现从x<3,y<3的五人中抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.
分析:(I)频率等于频数除以样本容量,求出各组的频率.以频率为纵坐标,画出出频率分布直方图.
(II)先求出服务满意度”为3时的5个数据的平均数,再利用标准差公式计算.
(III)此概型为古典概型,按照古典概型计算方法解决.
(II)先求出服务满意度”为3时的5个数据的平均数,再利用标准差公式计算.
(III)此概型为古典概型,按照古典概型计算方法解决.
解答:解:(I)“价格满意度”为1,2,3,4,5的频率分别为0.1,0.2,0.3,0.3.0.1.

(II)“服务满意度”为3时的5个数据的平均数为(3+7+8+8+4)÷5=6
所以标准差s=
=
≈2.1
(III)“服务满意度”为2的三人分别记为a,b,c.“服务满意度”为1的两人分别记为 m,n.
记“从x<3,y<3的五人中抽取两人征求意见,至少有一人的“服务满意度”为1为事件A,基本事件:(a,b),(a,c),(a,m),(a,n),(b,c),(b,m),(b,n),(c,m),(c,n)(m,n)共10个,
而事件A包含的基本事件有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n)(m,n)共7个,所以“从x<3,y<3的五人中抽取两人征求意见,至少有一人的“服务满意度”为1的概率为
.

(II)“服务满意度”为3时的5个数据的平均数为(3+7+8+8+4)÷5=6
所以标准差s=
|
| 4.4 |
(III)“服务满意度”为2的三人分别记为a,b,c.“服务满意度”为1的两人分别记为 m,n.
记“从x<3,y<3的五人中抽取两人征求意见,至少有一人的“服务满意度”为1为事件A,基本事件:(a,b),(a,c),(a,m),(a,n),(b,c),(b,m),(b,n),(c,m),(c,n)(m,n)共10个,
而事件A包含的基本事件有(a,m),(a,n),(b,m),(b,n),(c,m),(c,n)(m,n)共7个,所以“从x<3,y<3的五人中抽取两人征求意见,至少有一人的“服务满意度”为1的概率为
| 7 |
| 10 |
点评:本题考查了频率分布直方图,标准差,古典概型.融合了几个基本知识点,是好题.

练习册系列答案
相关题目
合肥一中为了了解学校食堂的服务质量情况,对在校就餐的1400名学生按5%的比例进行问卷调查,把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如下表所示(服务满意度为x,价格满意度为y).
(I)作出“价格满意度”的频率分布直方图;

(II)求“服务满意度”为3时的5个“价格满意度”数据的标准差;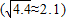
(III)为改进食堂服务质量,现从x<3,y<3的五人中抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.
人数 y x | 价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服 务 满 意 度 | 1 | 1 | 1 | 2 | 2 | |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 1 | 2 | 3 | 1 | ||

(II)求“服务满意度”为3时的5个“价格满意度”数据的标准差;
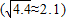
(III)为改进食堂服务质量,现从x<3,y<3的五人中抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.
合肥一中为了了解学校食堂的服务质量情况,对在校就餐的1400名学生按5%的比例进行问卷调查,把学生对食堂的“服务满意度”与“价格满意度”都分为五个等级:1级(很不满意);2级(不满意);3级(一般);4级(满意);5级(很满意),其统计结果如下表所示(服务满意度为x,价格满意度为y).
(I)作出“价格满意度”的频率分布直方图;
(II)求“服务满意度”为3时的5个“价格满意度”数据的标准差;
(III)为改进食堂服务质量,现从x<3,y<3的五人中抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.
人数 y x | 价格满意度 | |||||
| 1 | 2 | 3 | 4 | 5 | ||
| 服 务 满 意 度 | 1 | 1 | 1 | 2 | 2 | |
| 2 | 2 | 1 | 3 | 4 | 1 | |
| 3 | 3 | 7 | 8 | 8 | 4 | |
| 4 | 1 | 4 | 6 | 4 | 1 | |
| 5 | 1 | 2 | 3 | 1 | ||

(II)求“服务满意度”为3时的5个“价格满意度”数据的标准差;

(III)为改进食堂服务质量,现从x<3,y<3的五人中抽取两人征求意见,求至少有一人的“服务满意度”为1的概率.