题目内容
已知数列{an}中,a1=1,且点P(an,an+1)(n∈N*)在直线x-y+1=0上.(1)求数列{an}的通项公式;
(2)若函数
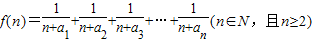 ,求函数f(n)的最小值;
,求函数f(n)的最小值;(3)设
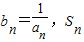 表示数列{bn}的前项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
表示数列{bn}的前项和.试问:是否存在关于n的整式g(n),使得S1+S2+S3+…+Sn-1=(Sn-1)•g(n)对于一切不小于2的自然数n恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试说明理由.
【答案】分析:(1)把点P代入直线方程,可得an+1-an=1进而判断数列{an}是以1为首项,1为公差的等差数列数列{an}的通项公式可得.
(2)分别表示出f(n)和f(n+1),通过f(n+1)-f(n)>0判断f(n)单调递增,故f(n)的最小值是
(3)把(1)中的an代入求得bn,进而求得 最后(n-1)Sn-1-(n-2)Sn-2=nSn-n=n(Sn-1),判断存在关于n的整式g(x)=n.
最后(n-1)Sn-1-(n-2)Sn-2=nSn-n=n(Sn-1),判断存在关于n的整式g(x)=n.
解答:解:(1)由点P(an,an+1)在直线x-y+1=0上,
即an+1-an=1,且a1=1,数列{an}是以1为首项,
1为公差的等差数列an=1+(n-1)•1=n(n≥2),
a1=1同样满足,所以an=n
(2)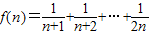
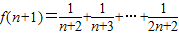
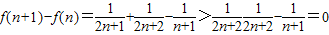
所以f(n)是单调递增,故f(n)的最小值是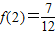
(3)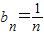 ,可得
,可得 ,
,

∴nSn-(n-1)Sn-1=Sn-1+1,
∴(n-1)Sn-1-(n-2)Sn-2=Sn-2+1
…
S2-S1=S1+1
∴nSn-S1=S1+S2+S3+…+Sn-1+n-1
∴S1+S2+S3+…+Sn-1=nSn-n=n(Sn-1),n≥2
∴g(n)=n
故存在关于n的整式g(x)=n,
使得对于一切不小于2的自然数n恒成立.
点评:本题主要考查了等差数列的通项公式.即数列与不等式相结合的问题考查,考查了学生综合思维能力.
(2)分别表示出f(n)和f(n+1),通过f(n+1)-f(n)>0判断f(n)单调递增,故f(n)的最小值是

(3)把(1)中的an代入求得bn,进而求得
 最后(n-1)Sn-1-(n-2)Sn-2=nSn-n=n(Sn-1),判断存在关于n的整式g(x)=n.
最后(n-1)Sn-1-(n-2)Sn-2=nSn-n=n(Sn-1),判断存在关于n的整式g(x)=n.解答:解:(1)由点P(an,an+1)在直线x-y+1=0上,
即an+1-an=1,且a1=1,数列{an}是以1为首项,
1为公差的等差数列an=1+(n-1)•1=n(n≥2),
a1=1同样满足,所以an=n
(2)
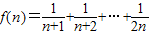
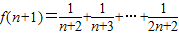
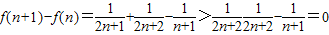
所以f(n)是单调递增,故f(n)的最小值是
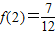
(3)
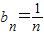 ,可得
,可得 ,
,
∴nSn-(n-1)Sn-1=Sn-1+1,
∴(n-1)Sn-1-(n-2)Sn-2=Sn-2+1
…
S2-S1=S1+1
∴nSn-S1=S1+S2+S3+…+Sn-1+n-1
∴S1+S2+S3+…+Sn-1=nSn-n=n(Sn-1),n≥2
∴g(n)=n
故存在关于n的整式g(x)=n,
使得对于一切不小于2的自然数n恒成立.
点评:本题主要考查了等差数列的通项公式.即数列与不等式相结合的问题考查,考查了学生综合思维能力.

练习册系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|