题目内容
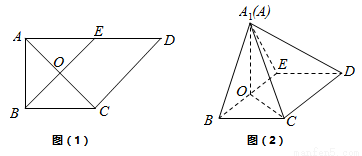
如图(1)在直角梯形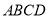 中,
中, ,
,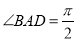 ,
,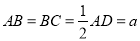 ,
, 是
是 的中点,
的中点,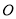 是
是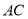 与
与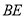 的交点,将△
的交点,将△ 沿
沿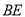 折起到图(2)中△
折起到图(2)中△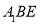 的位置,得到四棱锥
的位置,得到四棱锥
 .
.
(1)求证: 平面
平面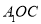 ;
;
(2)当平面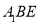 ⊥平面
⊥平面 时,四棱锥
时,四棱锥 的体积为
的体积为 ,求
,求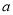 的值.
的值.
练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
题目内容
如图(1)在直角梯形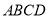 中,
中, ,
,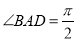 ,
,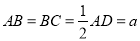 ,
, 是
是 的中点,
的中点,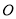 是
是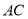 与
与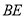 的交点,将△
的交点,将△ 沿
沿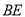 折起到图(2)中△
折起到图(2)中△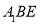 的位置,得到四棱锥
的位置,得到四棱锥
 .
.

(1)求证: 平面
平面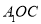 ;
;
(2)当平面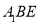 ⊥平面
⊥平面 时,四棱锥
时,四棱锥 的体积为
的体积为 ,求
,求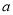 的值.
的值.
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案