题目内容
1.一次函数的图象过点(2,0),和(-2,1),则此函数的解析式为y=$-\frac{1}{4}x$$+\frac{1}{2}$.分析 可设一次函数为y=ax+b,根据该函数的图象过点(2,0)和(-2,1),从而将这两点坐标带入y=ax+b便可得出关于a,b的二元一次方程组,解出a,b便可得到该函数的解析式.
解答 解:设一次函数为y=ax+b;
∵该函数过点(2,0),(-2,1);
∴$\left\{\begin{array}{l}{2a+b=0}\\{-2a+b=1}\end{array}\right.$;
解得,$a=-\frac{1}{4},b=\frac{1}{2}$;
∴该函数的解析式为:y=$-\frac{1}{4}x+\frac{1}{2}$.
故答案为:$y=-\frac{1}{4}x+\frac{1}{2}$.
点评 考查一次函数的一般形式,待定系数求函数解析式的方法,清楚函数图象上的点和函数解析式的关系.

练习册系列答案
相关题目
12.关于x的方程x2+kx-k=0有两个不相等的实数根x1,x2,且满足1<x1<2<x2<3,则实数k的取值范围是( )
| A. | $({-\frac{9}{2},-4})$ | B. | $({4,\frac{9}{2}})$ | C. | (-6,-4) | D. | $({-4,\frac{4}{3}})$ |
6.已知椭圆的对称轴是坐标轴,离心率e=$\frac{2}{3}$,长轴长为6,则椭圆的方程( )
| A. | $\frac{{x}^{2}}{36}+\frac{{y}^{2}}{20}=1$ | B. | $\frac{{x}^{2}}{36}+\frac{{y}^{2}}{20}=1或\frac{{x}^{2}}{20}+\frac{{y}^{2}}{36}=1$ | ||
| C. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1$ | D. | $\frac{{x}^{2}}{9}+\frac{{y}^{2}}{5}=1或\frac{{x}^{2}}{5}+\frac{{y}^{2}}{9}=1$ |
13.设函数f(x)=x2-1,对任意x∈[$\frac{3}{2}$,+∞),f($\frac{x}{m}$)-4m2f(x)≤f(x-1)+4f(m)恒成立,则实数m的取值范围是( )
| A. | [-$\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{2}$] | B. | [$\frac{3}{2}$,+∞) | C. | (0,$\frac{3}{2}$] | D. | (-∞,-$\frac{\sqrt{3}}{2}$]∪[$\frac{\sqrt{3}}{2}$,+∞) |
11.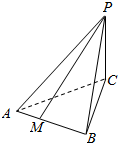 已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )
已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )
 已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )
已知三棱锥P-ABC如图所示,平面PAC⊥平面ABC,正三角形ABC的面积为9$\sqrt{3}$,PC=4,PA=2$\sqrt{13}$,M是AB边上的一动点,则PM的最小值为( )| A. | 2$\sqrt{43}$ | B. | $\sqrt{43}$ | C. | $\sqrt{11}$ | D. | 2$\sqrt{11}$ |
