题目内容
设集合Sn={1,2,3,,n),若X是Sn的子集,把X中所有元素的和称为X的“容量”(规定空集的容量为0),若X的容量为奇(偶)数,则称X为Sn的奇(偶)子集.
(I)写出S4的所有奇子集;
(Ⅱ)求证:Sn的奇子集与偶子集个数相等;
(Ⅲ)求证:当n≥3时,Sn的所有奇子集的容量之和等于所有偶子集的容量之和.
【答案】
(I)详见解析;(Ⅱ)详见解析;(Ⅲ)详见解析
【解析】
试题分析:(I)根据奇子集的定义可直接得出,注意应按规律一一列出以防重写或漏写。(Ⅱ)取Sn的任意一个奇子集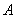 可能含有1也可能不含1,当奇子集
可能含有1也可能不含1,当奇子集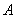 含有1时,令
含有1时,令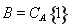 ,当奇子集
,当奇子集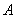 不含1时,令
不含1时,令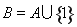 ,则
,则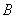 为
为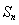 的偶子集,且
的偶子集,且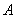 与
与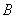 相对应,反之也成立。因为
相对应,反之也成立。因为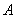 与
与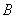 相对应即Sn的奇子集与偶子集个数相等。(Ⅲ)由(Ⅱ)知Sn的奇子集与偶子集个数相等,且Sn中每一个元素在奇子集与偶子集中出现的次数是相同的,所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
相对应即Sn的奇子集与偶子集个数相等。(Ⅲ)由(Ⅱ)知Sn的奇子集与偶子集个数相等,且Sn中每一个元素在奇子集与偶子集中出现的次数是相同的,所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
试题解析:(I)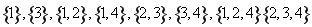
(Ⅱ)对于Sn的每个奇子集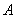 ,
,
当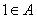 时,取
时,取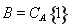 ;当
;当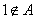 时,取
时,取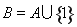 。
。
则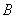 为
为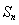 的偶子集。
的偶子集。
反之,若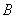 为
为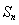 的偶子集,
的偶子集,
当 时,取
时,取 ;当
;当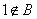 时,取
时,取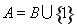 。
。
则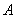 为
为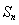 的奇子集。
的奇子集。
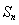 的奇子集与偶子集之间建立了一一对应的关系,所以
的奇子集与偶子集之间建立了一一对应的关系,所以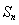 的奇子集和偶子集的个数相等。
的奇子集和偶子集的个数相等。
(Ⅲ)对于任意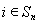 ,
,
当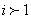 时,含
时,含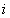 的
的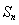 的子集共有
的子集共有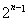 个。由(Ⅱ)可知,对每个数
个。由(Ⅱ)可知,对每个数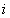
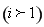 ,在奇子集与偶子集中,
,在奇子集与偶子集中,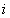 所占的个数是相等的;
所占的个数是相等的;
当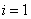 时,将(Ⅱ)中的1换成3即可。
时,将(Ⅱ)中的1换成3即可。
可知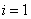 在奇子集与偶子集中占的个数是相等。
在奇子集与偶子集中占的个数是相等。
综合(1)(2),每个元素都是在奇子集与偶子集中占的个数相等。
所以Sn的所有奇子集的容量之和等于所有偶子集的容量之和。
考点:新概念问题。

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目