题目内容
(本小题满分13分)设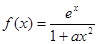 ,其中
,其中 为正实数。
为正实数。
(1)当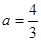 时,求
时,求 的极值点;
的极值点;
(2)若 为R上的单调函数,求
为R上的单调函数,求 的取值范围。
的取值范围。
(Ⅰ)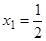 是
是 的极大值点,
的极大值点, 是
是 的极小值点.(Ⅱ)
的极小值点.(Ⅱ) .
.
解析试题分析:(Ⅰ)当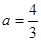 时,
时, ,
,
令 得
得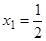 ,
, ,又由
,又由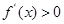 得
得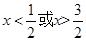 ;由
;由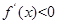 得
得 。
。
所以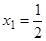 是
是 的极大值点,
的极大值点, 是
是 的极小值点.
的极小值点.
(Ⅱ)因为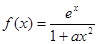 ,所以
,所以 ,
,
若 为R上的单调函数,则
为R上的单调函数,则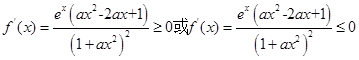 恒成立且不恒为0.又
恒成立且不恒为0.又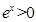 ,所以只需
,所以只需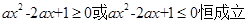 且不恒为0 。
且不恒为0 。
因为 为正实数,所以只需
为正实数,所以只需 且不恒为0,所以
且不恒为0,所以 ,解得
,解得 .
.
考点:利用导数研究函数的极值点;利用导数研究函数的单调性。
点评:此题的第二问是易错题,我们要注意:由“ 为R上的单调函数”应得到的是“
为R上的单调函数”应得到的是“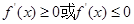 在R上恒成立且不恒为0”。社道题是导数中的典型题目。我们一定要熟练掌握。
在R上恒成立且不恒为0”。社道题是导数中的典型题目。我们一定要熟练掌握。

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目

 的最小正周期.
的最小正周期. 时,求函数
时,求函数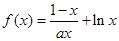
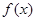 在
在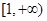 上为增函数,求正实数
上为增函数,求正实数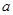 的取值范围;
的取值范围;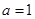 时,求
时,求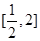 上的最大值和最小值;
上的最大值和最小值;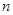 ,都有
,都有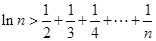 。
。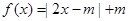 .
. 的解集为
的解集为 ,求实数
,求实数 的值;
的值;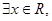 使
使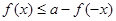 能成立,求实数a的取值范围.
能成立,求实数a的取值范围. 元,若销售价为
元,若销售价为 元,可卖出
元,可卖出 元,销售量就减少
元,销售量就减少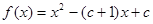
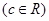 .
. 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围; 在点
在点 处的切线方程为
处的切线方程为 .
. 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 都有
都有 ,求实数
,求实数 的最小值;
的最小值; 的函数
的函数 是奇函数.
是奇函数. 的值;
的值; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. 的定义域.
的定义域.