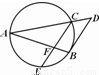
题目内容
(不等式选讲选做题)x、y>0,x+y=1,则(x+| 1 |
| x |
| 1 |
| y |
分析:先将式子展开,利用完全平方公式将x2+y2用(x+y)2表示,将x+y用1代替;令xy=t;将函数转化为只含t的函数;利用基本不等式求出t的范围;利用函数的单调性求出最小值.
解答:解:(x+
)(y+
)=xy+
+
+
=
=
=xy+
-2
∵x+y=1
∴xy≤(
)2=
令xy=t则0<t≤
∴(x+
)(y+
)=t+
-2
∵t+
-2在(0,
]递减
当t=
最小为
故答案为
| 1 |
| x |
| 1 |
| y |
| x |
| y |
| y |
| x |
| 1 |
| xy |
| x2y2+x2+y2+1 |
| xy |
=
| x2y2+(x+y)2-2xy+1 |
| xy |
=xy+
| 2 |
| xy |
∵x+y=1
∴xy≤(
| x+y |
| 2 |
| 1 |
| 4 |
令xy=t则0<t≤
| 1 |
| 4 |
∴(x+
| 1 |
| x |
| 1 |
| y |
| 2 |
| t |
∵t+
| 2 |
| t |
| 1 |
| ,4 |
当t=
| 1 |
| 4 |
| 25 |
| 4 |
故答案为
| 25 |
| 4 |
点评:本题考查换元的数学思想方法:注意新变量的范围、考查利用基本不等式求代数式的范围、考查利用函数单调性求函数的最值.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 ,则线段CD的长为 .
,则线段CD的长为 .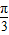 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .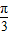 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .