题目内容
已知函数![]() 和
和![]() .其中
.其中![]() .
.
(Ⅰ)若函数![]() 与
与![]() 的图像的一个公共点恰好在x轴上,求
的图像的一个公共点恰好在x轴上,求![]() 的值;
的值;
(Ⅱ)若函数![]() 与
与![]() 图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的
图像相交于不同的两点A、B,O为坐标原点,试问:△OAB的面积S有没有最值?如果有,求出最值及所对应的![]() 的值;如果没有,请说明理由.
的值;如果没有,请说明理由.
(Ⅲ)若![]() 和
和![]() 是方程
是方程![]() 的两根,且满足
的两根,且满足![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
解:(Ⅰ)设函数![]() 图像与x轴的交点坐标为(
图像与x轴的交点坐标为(![]() ,0),
,0),
又∵点(![]() ,0)也在函数
,0)也在函数![]() 的图像上,∴
的图像上,∴![]() .
.
而![]() ,∴
,∴![]() .
.
(Ⅱ)依题意,![]() ,即
,即![]() ,
,
整理,得 ![]() ,①
,①
∵![]() ,函数
,函数![]() 与
与![]() 图像相交于不同的两点A、B,
图像相交于不同的两点A、B,
∴![]() ,即△=
,即△=![]() =
=![]() =(3
=(3![]() -1)(-
-1)(-![]() -1)>0.
-1)>0.
∴-1<![]() <
<![]() 且
且![]() .
.
设A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() ),且
),且![]() <
<![]() ,由①得,
,由①得,![]()
![]() =1>0,
=1>0, ![]() .
.
设点o到直线![]() 的距离为d,
的距离为d,
则![]() ,
,![]() .
.
∴![]() =
=![]()
![]()
![]()
=![]()
![]() .
.
∵-1<![]() <
<![]() 且
且![]() ,∴当
,∴当![]() 时,
时,![]() 有最大值
有最大值![]() ,
,![]() 无最小值.
无最小值.
(Ⅲ)由题意可知![]() .
.
![]() ,∴
,∴![]() ,∴当
,∴当![]() 时,
时,![]()
即![]() .
.
又![]() ,
,
![]() ∴
∴![]() <0, ∴
<0, ∴![]() ,
,
综上可知,![]() .
.

练习册系列答案
相关题目
 和
和 .其中
.其中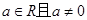 .
. 与
与 的图像的一个公共点恰好在x轴上,求
的图像的一个公共点恰好在x轴上,求 的值;w
的值;w  和
和 是方程
是方程 的两根,且满足
的两根,且满足 ,
, 时,
时, .
.