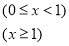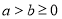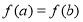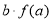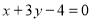题目内容
经市场调查,某种商品在过去50天的销售量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N).前30天价格为g(t)=t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系;
(2)求日销售额S的最大值.
(1) ;(2)日销售额
;(2)日销售额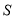 有最大值6400.
有最大值6400.
【解析】
试题分析:(1)商品的日销售额=销售量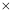 价格,即
价格,即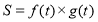 ,因为前30天的价格与后20天的价格不同,故
,因为前30天的价格与后20天的价格不同,故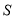 为一个分段函数;
为一个分段函数;
(2)先分别求出两段函数的最大值,一段是二次函数可用配方法,结合定义域的范围,可知最大值在对称轴处取得,令一段是一次函数且为单调减函数,最大值在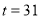 取得,要注意
取得,要注意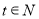 ,再比较哪一个值最大,即为
,再比较哪一个值最大,即为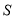 的最大值.
的最大值.
试题解析:(1)根据题意,得
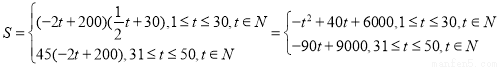
(2)①当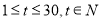 时,
时,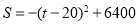 ,
,
∴当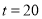 时,
时,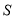 的最大值为6400
的最大值为6400
②当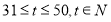 时,
时,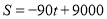 为减函数,
为减函数,
∴当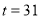 时,
时,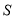 的最大值为6210.
的最大值为6210.
∵6210<6400,∴当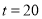 时,日销售额
时,日销售额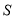 有最大值6400.
有最大值6400.
考点:1、函数的实际应用;2、分段函数求最值;3、二次函数、一次函数求最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目