题目内容
双曲线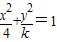 的离心率e∈(1,2),则k的取值范围是( )
的离心率e∈(1,2),则k的取值范围是( )A.(-∞,0)
B.(-3,0)
C.(-12,0)
D.(-60,-12)
【答案】分析:先把双曲线方程化为标准形式,由离心率的范围求出k的取值范围.
解答:解:∵双曲线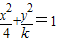 的离心率e∈(1,2),
的离心率e∈(1,2),
∴双曲线标准方程为: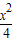 -
-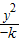 =1∴k<0,
=1∴k<0,
∴1<e2<4,1< <4,-12<k<0,
<4,-12<k<0,
故答案选 C
点评:本题考查双曲线的标准方程和离心率.
解答:解:∵双曲线
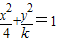 的离心率e∈(1,2),
的离心率e∈(1,2),∴双曲线标准方程为:
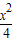 -
-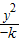 =1∴k<0,
=1∴k<0,∴1<e2<4,1<
 <4,-12<k<0,
<4,-12<k<0,故答案选 C
点评:本题考查双曲线的标准方程和离心率.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
已知点F1、F2分别是双曲线
-
=1的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若△ABF2为锐角三角形,则该双曲线的离心率e的取值范围是( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、(1,+∞) | ||
B、(1,
| ||
| C、(1,2) | ||
D、(1,1+
|