题目内容
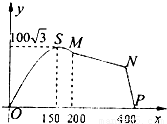
如图,顺达架校拟在长为400m的道路OP的一侧修建一条训练道路,训练道路的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),x∈[0,200]的图象,且图象的最高点为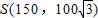 ,训练道路的后一部分为折线段MNP,为保证训练安全,限定∠MNP=120°.
,训练道路的后一部分为折线段MNP,为保证训练安全,限定∠MNP=120°.(I)求曲线段OSM对应函数的解析式;
(II)应如何设计,才能使折线段训练道路MNP最长?最长为多少?
【答案】分析:(I)由题意可得,最高点S(150,100 ),故A=100
),故A=100 ,由
,由  •
•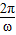 =150 求得ω,即可得到函数的解析式.
=150 求得ω,即可得到函数的解析式.
(II)当x=200时,y=150,故MP=250,设MN=m,NP=n,在△MNP中,由余弦定理可得=2502=(m+n)2-mn.由于 mn≤ ,当且仅当m=n时,取等号,可得0<m+n≤
,当且仅当m=n时,取等号,可得0<m+n≤ ,从而求得 m+n的最大值.
,从而求得 m+n的最大值.
解答:解:(I)由题意可得,最高点S(150,100 ),故A=100
),故A=100 ,
, •
• =150,ω=
=150,ω= .
.
故函数的解析式为 y=100 sin
sin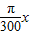 (0≤x≤200).
(0≤x≤200).
(II)当x=200时,y=150,故MP= =250,设MN=m,NP=n,在△MNP中,由余弦定理可得
=250,设MN=m,NP=n,在△MNP中,由余弦定理可得
MP2=2502=MN2+NP2-2MN•NP•cos120°=m2+n2+mn=(m+n)2-mn.
由于 mn≤ ,当且仅当m=n时,取等号,∴2502=(m+n)2-mn≥(m+n)2-
,当且仅当m=n时,取等号,∴2502=(m+n)2-mn≥(m+n)2- ,
,
故有 0<m+n≤ ,即将折线段中MN与NP的长度设计为相等时,折线段训练道路MNP最长,
,即将折线段中MN与NP的长度设计为相等时,折线段训练道路MNP最长,
且最长为 米.
米.
点评:本题主要考查解三角形的实际应用,余弦定理,以及基本不等式的应用,体现了数形结合的数学思想,属于难题.
 ),故A=100
),故A=100 ,由
,由  •
•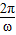 =150 求得ω,即可得到函数的解析式.
=150 求得ω,即可得到函数的解析式.(II)当x=200时,y=150,故MP=250,设MN=m,NP=n,在△MNP中,由余弦定理可得=2502=(m+n)2-mn.由于 mn≤
 ,当且仅当m=n时,取等号,可得0<m+n≤
,当且仅当m=n时,取等号,可得0<m+n≤ ,从而求得 m+n的最大值.
,从而求得 m+n的最大值.解答:解:(I)由题意可得,最高点S(150,100
 ),故A=100
),故A=100 ,
, •
• =150,ω=
=150,ω= .
.故函数的解析式为 y=100
 sin
sin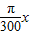 (0≤x≤200).
(0≤x≤200).(II)当x=200时,y=150,故MP=
 =250,设MN=m,NP=n,在△MNP中,由余弦定理可得
=250,设MN=m,NP=n,在△MNP中,由余弦定理可得MP2=2502=MN2+NP2-2MN•NP•cos120°=m2+n2+mn=(m+n)2-mn.
由于 mn≤
 ,当且仅当m=n时,取等号,∴2502=(m+n)2-mn≥(m+n)2-
,当且仅当m=n时,取等号,∴2502=(m+n)2-mn≥(m+n)2- ,
,故有 0<m+n≤
 ,即将折线段中MN与NP的长度设计为相等时,折线段训练道路MNP最长,
,即将折线段中MN与NP的长度设计为相等时,折线段训练道路MNP最长,且最长为
 米.
米.点评:本题主要考查解三角形的实际应用,余弦定理,以及基本不等式的应用,体现了数形结合的数学思想,属于难题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
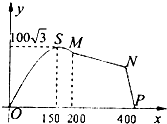 如图,顺达架校拟在长为400m的道路OP的一侧修建一条训练道路,训练道路的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),x∈[0,200]的图象,且图象的最高点为
如图,顺达架校拟在长为400m的道路OP的一侧修建一条训练道路,训练道路的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0),x∈[0,200]的图象,且图象的最高点为