题目内容
一轮船从A点沿北偏东70°的方向行10海里至海岛B,又从B沿北偏东10°的方向行10海里至海岛C,若此轮船从A点直接沿直线行至海岛C,则此轮船沿( )方向行驶( )海里至海岛C.
A.北偏东50°;10 B.北偏东40°;10
B.北偏东40°;10
C.北偏东30°;10 D.北偏东20°;10
D.北偏东20°;10
A.北偏东50°;10
 B.北偏东40°;10
B.北偏东40°;10
C.北偏东30°;10
 D.北偏东20°;10
D.北偏东20°;10
B
解:因为利用解三角形正弦定理和余弦定理可知一轮船从A点沿北偏东70°的方向行10海里至海岛B,又从B沿北偏东10°的方向行10海里至海岛C,若此轮船从A点直接沿直线行至海岛C则向北偏东40°;10


练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
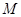 是△
是△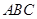 内的一点(不在边界上),定义
内的一点(不在边界上),定义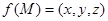 ,其中
,其中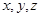 分别表示△
分别表示△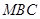 ,△
,△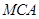 ,△
,△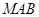 的面积,若
的面积,若 ,则
,则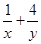 的最小值为( )
的最小值为( ) 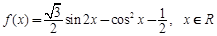 .]
.]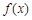 的最小值和最小正周期;
的最小值和最小正周期;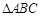 的内角
的内角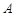 、
、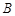 、
、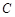 的对边分别为
的对边分别为 ,
,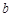 ,
,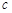 ,且
,且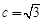 ,
,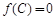 ,
,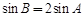 ,求
,求 满足
满足 若
若 ,
, 且
且 满足:
满足: ,
, ,
, 为
为 与
与 的夹角.
的夹角. ;
; ;
;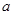 ,
,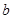 ,
,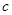 分别为
分别为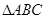 三个内角
三个内角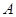 ,
,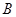 ,
,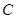 的对边,
的对边,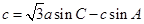 .
.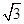 ,求
,求 是底部
是底部 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物, 为塔的最高点.现需在对岸测出塔高
为塔的最高点.现需在对岸测出塔高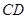 ,使
,使 三点不在同一
三点不在同一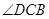 及
及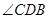 的大小(分别用
的大小(分别用 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用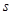 表示测得的数据),另外需在点
表示测得的数据),另外需在点 测得塔顶
测得塔顶 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高 ,使
,使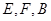 三点在同一条直线上.在
三点在同一条直线上.在 处分别测得塔顶
处分别测得塔顶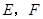 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高
 中,三边之比
中,三边之比 ,则最大角的余弦值等于 ( )
,则最大角的余弦值等于 ( )




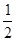 ,cosB=
,cosB=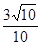 .
.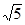 ,求最长边的长.
,求最长边的长. 中,若
中,若 ,则
,则