题目内容
设二次函数 y=f(x)=ax2+bx+c的图象以y轴为对称轴,已知a+b=1,而且若点(x,y)在 y=f(x)的图象上,则点(x,y2+1)在函数 g(x)=f[f(x)]的图象上.(1)求g(x)的解析式;
(2)设F(x)=g(x)-λf(x),问是否存在这样的l(λ∈R),使f(x)在
 内是减函数,在(
内是减函数,在( ,0)内是增函数.
,0)内是增函数.
【答案】分析:(1)根据二次函数 f(x)=ax2+bx+c的图象以y轴为对称轴,得到b=0,,又a+b=1,求得a=1,再根据点(x,y)在 y=f(x)的图象上,则点(x,y2+1)在函数 g(x)=f[f(x)]的图象上,代入,即可求得c的值,从而求得函数g(x)的解析式;
(2)根据(1)的结果,假设存在λ满足题意,即说明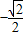 是函数的一个极小值点,求导,即
是函数的一个极小值点,求导,即 是导函数的一个零点,解方程即可求得λ的值,注意验证.
是导函数的一个零点,解方程即可求得λ的值,注意验证.
解答:解:(1)∵二次函数 f(x)=ax2+bx+c的图象以y轴为对称轴,
∴b=0,又∵a+b=1,∴a=1,
∴f(x)=x2+c,
∵点(x,y)在 y=f(x)的图象上,则点(x,y2+1)在函数 g(x)=f[f(x)]的图象上,
∴y2+1=(x+c)2+c,即(x2+c)2+1=(x+c)2+c,
c=1,
∴f(x)=x2+1;g(x)=(x2+1)2+1;
(2)假设存在λ,使得F(x)在( 内是减函数,在(
内是减函数,在( ,0)内是增函数,
,0)内是增函数,
而 是函数的一个极小值点,F(x)=(x2+1)2+1-λ(x2+1),
是函数的一个极小值点,F(x)=(x2+1)2+1-λ(x2+1),
F′(x)=4x(x2+1)-2λx,∴F( )=0,解得λ=3,
)=0,解得λ=3,
经检验知λ=3复合题意,
故λ=3.
点评:此题是个中档题.考查待定系数法求函数解析式,以及利用导数研究函数的单调性和极值问题,体现了转化的思想,其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.
(2)根据(1)的结果,假设存在λ满足题意,即说明
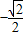 是函数的一个极小值点,求导,即
是函数的一个极小值点,求导,即 是导函数的一个零点,解方程即可求得λ的值,注意验证.
是导函数的一个零点,解方程即可求得λ的值,注意验证.解答:解:(1)∵二次函数 f(x)=ax2+bx+c的图象以y轴为对称轴,
∴b=0,又∵a+b=1,∴a=1,
∴f(x)=x2+c,
∵点(x,y)在 y=f(x)的图象上,则点(x,y2+1)在函数 g(x)=f[f(x)]的图象上,
∴y2+1=(x+c)2+c,即(x2+c)2+1=(x+c)2+c,
c=1,
∴f(x)=x2+1;g(x)=(x2+1)2+1;
(2)假设存在λ,使得F(x)在(
 内是减函数,在(
内是减函数,在( ,0)内是增函数,
,0)内是增函数,而
 是函数的一个极小值点,F(x)=(x2+1)2+1-λ(x2+1),
是函数的一个极小值点,F(x)=(x2+1)2+1-λ(x2+1),F′(x)=4x(x2+1)-2λx,∴F(
 )=0,解得λ=3,
)=0,解得λ=3,经检验知λ=3复合题意,
故λ=3.
点评:此题是个中档题.考查待定系数法求函数解析式,以及利用导数研究函数的单调性和极值问题,体现了转化的思想,其中问题(2)是一个开放性问题,考查了同学们观察、推理以及创造性地分析问题、解决问题的能力.

练习册系列答案
相关题目