题目内容
(不等式选讲选做题) 已知a,b,c∈R,且a+b+c=2,a2+2b2+3c2=4,则a的取值范围为分析:由4-a2=(2b2+3c2)×1=
(2b2+3c2)(
+
)≥(b+c)2•
=(a-2)2•
.得到关于a的不等关系:20-5a2≥6(a2-4a+4)解之即得a的取值范围.
| 6 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
| 6 |
| 5 |
| 6 |
| 5 |
解答:解:由4-a2=(2b2+3c2)×1=
(2b2+3c2)(
+
)
≥(b+c)2•
=(a-2)2•
.
∴20-5a2≥6(a2-4a+4)
∴11a2-24a+4≤0,
∴
≤a≤2.
则a的取值范围为[
,2].
故答案为:[
,2].
| 6 |
| 5 |
| 1 |
| 2 |
| 1 |
| 3 |
≥(b+c)2•
| 6 |
| 5 |
| 6 |
| 5 |
∴20-5a2≥6(a2-4a+4)
∴11a2-24a+4≤0,
∴
| 2 |
| 11 |
则a的取值范围为[
| 2 |
| 11 |
故答案为:[
| 2 |
| 11 |
点评:此题主要考查不等式的证明问题,其中涉及到柯西不等式和基本不等式的应用问题,有一定的技巧性,需要同学们对一般形式的柯西不等式非常熟练.

练习册系列答案
相关题目
 ,则线段CD的长为 .
,则线段CD的长为 .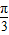 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 .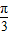 )的直角坐标是 .
)的直角坐标是 .
 ,则线段CD的长为 .
,则线段CD的长为 . )的直角坐标是 .
)的直角坐标是 .