Question

已知点P（2，-3）、Q（3，2），直线ax-y+2=0与线段PQ相交，则a的取值范围是（　　）

• A、a≥

  4

  3

• B、a≤-

  4

  3

• C、-

  5

  2

  ≤a≤0
• D、a≤-

  4

  3

  或a≥

  1

  2

Answer 1

分析：首先将方程转化成点斜式，求出斜率以及交点坐标，画出图象，即可求出结果．

解答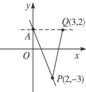：解：直线ax-y+2=0可化为y=ax+2，斜率k=a，恒过定点A（0，2）．
如图，直线与线段PQ相交，0≥k≥k_AP，即-

5

2

≤a≤0．
故选C．

点评：本题考查了直线的斜率，解题的关键是通过数形结合的方法求解，属于基础题．