题目内容
 (2012•许昌二模)如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上,
(2012•许昌二模)如图,已知⊙O1与⊙O2外切于点P,AB是两圆的外公切线,A,B为切点,AB与O1O2的延长线相交于点C,延长AP交⊙O2于点D,点E在AD延长线上,(1)求证:△ABP是直角三角形;
(2)若AB•AC=AP•AE,AP=4,PD=
| 9 |
| 4 |
| EC |
| AC |
分析:(1)要证明△ABP是直角三角形,可以根据切线的性质,证明∠APB=90°即可
(2)求
的值,可以找到它们与已知线段的关系,通过求PB,证明△PBC∽△APC得出.
(2)求
| EC |
| AC |
解答:(1)证明:连接PB,OA,OB,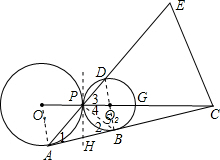
∵AB为公切线,∴∠1=
∠O1,∠2=
∠PO2B
∵O1A∥O2B,∴∠O1+∠PO2B=180°,∴∠1+∠2=90°,
∴∠APB=90°,∴△ABP是直角三角形.
(2)作内公切线PH,交AB于H,则AH=PH=HB,
∴∠APB=90°,∠DPB=90°,
∴DB为⊙O直径,∴DB⊥AB于B,∴Rt△ABD中,BP为斜边AD上的高,
∴PB2=AP•DP=4×
=9,∴PB=3,∵∠DBC=∠APB=90°,∠4=∠5,
∴∠DBC+∠5=∠APB+∠C,∴∠PBC=∠APC,
又∵∠6=∠6,∴△PBC∽△APC,∴
=
=
,
又∵BP⊥AE于P,∴∠3+∠4=90°,
∵AB为公切线,∴O2B⊥AB于B,∴∠2+∠5=90°,
又∵O2P=O2B,∴∠4=∠5,∴∠2=∠3.
由(1)知△APB∽△ACE,∴∠E=∠2,∴∠3=∠E,∴PC=EC.
∴
=
.

∵AB为公切线,∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∵O1A∥O2B,∴∠O1+∠PO2B=180°,∴∠1+∠2=90°,
∴∠APB=90°,∴△ABP是直角三角形.
(2)作内公切线PH,交AB于H,则AH=PH=HB,
∴∠APB=90°,∠DPB=90°,
∴DB为⊙O直径,∴DB⊥AB于B,∴Rt△ABD中,BP为斜边AD上的高,
∴PB2=AP•DP=4×
| 9 |
| 4 |
∴∠DBC+∠5=∠APB+∠C,∴∠PBC=∠APC,
又∵∠6=∠6,∴△PBC∽△APC,∴
| PC |
| AC |
| PB |
| AP |
| 3 |
| 4 |
又∵BP⊥AE于P,∴∠3+∠4=90°,
∵AB为公切线,∴O2B⊥AB于B,∴∠2+∠5=90°,
又∵O2P=O2B,∴∠4=∠5,∴∠2=∠3.
由(1)知△APB∽△ACE,∴∠E=∠2,∴∠3=∠E,∴PC=EC.
∴
| EC |
| AC |
| 3 |
| 4 |
点评:本题综合考查了圆与圆的位置关系、圆心角和圆周角的关系、切线的性质、相似三角形的判定和性质等多个知识点.

练习册系列答案
相关题目
 (2012•许昌二模)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.
(2012•许昌二模)如图,已知AB⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB,且F是CD的中点.