题目内容
当0＜x≤
时，8x＜logax，则a的取值范围是（ ）
| 1 |
| 3 |
分析：求出8x在0＜x≤
上的最大值，利用对数函数图象与性质求出a的范围即可．
| 1 |
| 3 |
解答：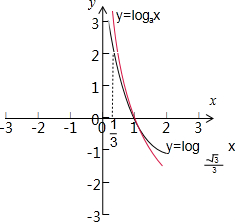
解：∵0＜x≤
，∴8x∈（1，2]，
又当0＜x≤
时，8x＜logax，
∴当0＜x≤
时，2＜logax，恒成立．如图：
a∈（0，1）对数函数是减函数，
∵log
=2，∴a∈(
，1)．
故选：B．
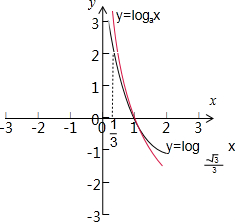解：∵0＜x≤| 1 |
| 3 |
又当0＜x≤
| 1 |
| 3 |
∴当0＜x≤
| 1 |
| 3 |
a∈（0，1）对数函数是减函数，
∵log
| ||
| 3 |
| 1 |
| 3 |
| ||
| 3 |
故选：B．
点评：本题考查指数、对数不等式的解法，对数函数的图象的应用，考查计算能力．
练习册系列答案
小题狂做系列答案
相关题目