题目内容

设函数定义域为R，当x<0时，f(x)>1，且对于任意的x∈R，有f(x + y)=f(x)•f(y)成立.数列{an}满足a1=f(0)，且f()=.问：是否存在正数k，使(1+均成立，若存在，求出k的最大值并证明，否则说明理由.

解：令x=-1,y=0,得f(-1)=f(-1)•f(0),

∵-1<0, ∴f(-1)>1, ∴f(0)=1,

∵f(0)=f(x)f(-x)  ∴f(x)>0  

设x1<x2  ∵x1-x2<0 ∴f(x1-x2)>1  

∴f(x1)=f(x1-x2)f(x2)  

∴f(x1)>f(x2)

∴f(x)是R上的减函数.

由,

∴

又∵a1=f(0)=1.  

∴{an}是等差数列，其首项为1，公差为d=2.∴an=2n-1.

∴存在正数k，使成立.

设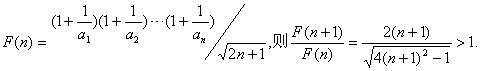

∴F(n)单调递增. ∴F(1)为F(n)的最小值.

由F(n)≥k恒成立. ∴k≤

∴k的最大值为

练习册系列答案
相关题目
奇函数y=f（x）的定义域为R，当x≥0时，f（x）=2x-x2，设函数y=f（x），x∈[a，b]的值域为[
1
b
，
1
a
]，则b的最小值为
 
．
设函数y=f（x）定义域为R，当x＜0时，f（x）＞1，且对于任意的x，y∈R，有f（x+y）=f（x）•f（y）成立．数列{an}满足a1=f（0），且 f(an+1)=
1
f(-2-an)
(n∈N*)．
（Ⅰ） 求f（0）的值；
（Ⅱ） 求数列{an}的通项公式；
（Ⅲ） 是否存在正数k，使(1+
1
a1
)(1+
1
a2
)…(1+
1
an
)≥k
2n+1
对一切n∈N*均成立，若存在，求出k的最大值，并证明，否则说明理由．
（附加题）设函数f（x）的定义域为R，当x＜0时，f（x）＞1，且对任意的x，y∈R，都有f（x+y）=f（x）f（y）．
（1）求f（0），判断函数f（x）的单调性；
（ 2 ）数列{an}满足a1=f（0），且f(an+1)=
1
f(-2-an)
（n∈N*）
A．求数列{an}的通项公式；
B．令bn=(
1
2
)an，Sn=b1+b2+b3+…bn，Tn=
1
a1a2
+
1
a2a3
+…+
1
anan+1
，试比较Sn与
2
3
Tn的大小，并加以证明．
（2013•营口二模）设函数f（x）的定义域为R，当x＜0时，f（x）＞1，且对于任意的实数x，y都有 f（x+y）=f（x）•f（y）成立，
（1）求f（0）的值，判断并证明函数f（x）的单调性；
（2）若数列{an}满足a1=f(0)，f(an+1)=
1
f(-2-an)
，(n∈N+)，求{an}的通项公式；
（3）如果f(1)=
1
2
，bn=lgf（an），求数列{bn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网