题目内容
16.若直线y=kx+1(k∈R)与椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$恒有公共点,求实数m的取值范围.分析 解法一、联立直线和椭圆方程,运用判别式非负,解不等式即可得到所求范围;
解法二、求出直线恒过定点,讨论椭圆的焦点位置,由直线和椭圆有交点,可得m的范围;
解法三、先根据直线方程可知直线恒过(0,1)点,要使直线y=kx+1与椭圆恒有公共点需(0,1)在椭圆上或椭圆内,进而求得m的范围
解答 解法一:由$\left\{{\begin{array}{l}{y=kx+1}\\{\frac{x^2}{5}+\frac{y^2}{m}=1}\end{array}}\right.$可得(5k2+m)x2+10kx+5-5m=0,
∴△=m-5k2-1≥0即m≥5k2+1≥1∴m≥1且m≠5;
解法二:直线恒过一定点(0,1),
当m<5时,椭圆焦点在x轴上,短半轴长$b=\sqrt{m}$,
要使直线与椭圆恒有交点则$\sqrt{m}≥1$,即1≤m<5;
当m>5时,椭圆焦点在y轴上,长半轴长$a=\sqrt{5}$,
可保证直线与椭圆恒有交点即m>5.
综述:m≥1且m≠5;
解法三:直线恒过一定点(0,1),
要使直线与椭圆恒有交点,
即要保证定点(0,1)在椭圆内部$\frac{0^2}{5}+\frac{1^2}{m}≤1$,
即m≥1且m≠5.
点评 本题主要考查了直线与椭圆有公共点的问题的解法,注意运用直线方程和椭圆方程联立,通过判别式非负解决,也可以通过直线恒过定点,证明定点在椭圆内,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
6.如果执行如图的程序框图,那么输出的值是( )
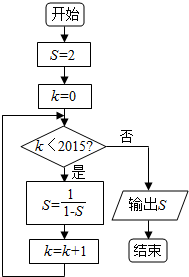

| A. | 2015 | B. | -1 | C. | $\frac{1}{2}$ | D. | 2 |
7.下列函数中,既是偶函数又在区间(0,+∞)上是增函数的是( )
| A. | y=-x2 | B. | y=ex-e-x | C. | y=ln(|x|+1) | D. | y=x•sinx+cosx |
1.在下列各结论中,正确的是( )
①“p∧q”为假是“p∨q”为假的充分不必要条件;
②“p∧q”为真是“p∨q”为真的充分不必要条件;
③“p∨q”为真是“?p”为假的必要不充分条件;
④“?p”为真是“p∧q”为假的必要不充分条件.
①“p∧q”为假是“p∨q”为假的充分不必要条件;
②“p∧q”为真是“p∨q”为真的充分不必要条件;
③“p∨q”为真是“?p”为假的必要不充分条件;
④“?p”为真是“p∧q”为假的必要不充分条件.
| A. | ①② | B. | ②④ | C. | ②③ | D. | ③④ |
6.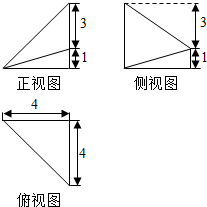 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )
 已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )
已知一个几何体的三视图如图所示,正视图、俯视图为直角三角形,侧视图是直角梯形,则它的体积等于( )| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{40}{3}$ | D. | .20 |