题目内容
已知数列 的通项公式是
的通项公式是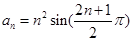 ,
,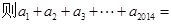 ( )
( )
A.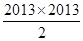 | B.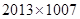 |
C. | D.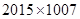 |
D
解析试题分析:化简可得: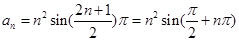 ,当n=2k-1时,
,当n=2k-1时,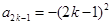 ,当n=2k时,
,当n=2k时,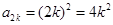 ,∴
,∴ ,所以
,所以
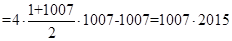 .
.
考点:数列求和.

练习册系列答案
相关题目
已知数列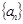 的前
的前 项和为
项和为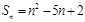 ,则数列
,则数列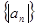 的前10项和为 ( )
的前10项和为 ( )
| A.56 | B.58 | C.62 | D.60 |
已知数列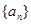 前n项和为
前n项和为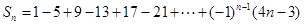 ,则
,则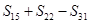 的值是( )
的值是( )
| A.13 | B.-76 | C.46 | D.76 |
数列 的通项公式
的通项公式 ,则该数列的前( )项之和等于
,则该数列的前( )项之和等于 .
.
A. | B. | C. | D. |
已知数列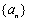 满足
满足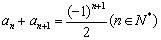 ,其中
,其中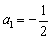 ,试通过计算
,试通过计算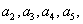 猜想
猜想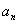 等于( )
等于( )
A.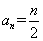 | B.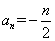 |
C.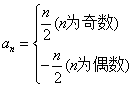 | D. |
(本小题满分12分)等比数列{an}的各项均为正数,且2a1+3a2=1,a=9a2a6.
(1)求数列{an}的通项公式;
(2)设bn=log3a1+log3a2+…+log3an,求数列 的前n项和.
的前n项和.
若数列{cn}的通项cn=(2n-1)·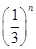 ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )
A.1-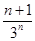 | B.1-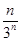 | C.1+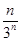 | D.1+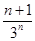 |
 对任意正整数n都成立,m为大于—1的非零常数。
对任意正整数n都成立,m为大于—1的非零常数。 是等比数列;
是等比数列;




 +
+ +
+ +…+
+…+ =( )
=( )


