题目内容
点M(a,b)是圆x2+y2=r2内异于圆心的一点,则直线ax+by=r2与圆的交点个数为( )
| A.0 | B.1 | C.2 | D.需讨论确定 |
A
因为点M(a,b)是圆内一点,所以a2+b2<r2.所以圆心到直线ax+by=r2的距离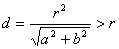 ,即直线与圆相离.故选A
,即直线与圆相离.故选A
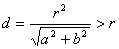 ,即直线与圆相离.故选A
,即直线与圆相离.故选A
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
 )且被圆x2+y2=25所截得的弦长是8,则l的方程为__________.
)且被圆x2+y2=25所截得的弦长是8,则l的方程为__________.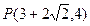 作一条直线和
作一条直线和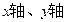 分别相交于
分别相交于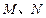 两点,试求
两点,试求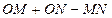 的最大值。(其中
的最大值。(其中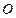 为坐标原点)
为坐标原点)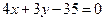 与圆心在原点的圆
与圆心在原点的圆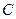 相切,求圆
相切,求圆 作直线
作直线 ,当斜率为何值时,直线
,当斜率为何值时,直线 有公共点.
有公共点.