题目内容
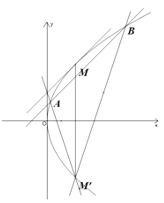
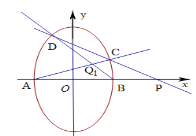
【题目】如图,设椭圆![]() 两顶点
两顶点![]() ,短轴长为4,焦距为2,过点
,短轴长为4,焦距为2,过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点.设直线
两点.设直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.
(1)求椭圆的方程;
(2)求线段![]() 中点
中点![]() 的轨迹方程;
的轨迹方程;
(3)求证:点![]() 的横坐标为定值.
的横坐标为定值.
【答案】(1)![]() ;(2)
;(2)![]() (
(![]() );(3)
);(3)![]() .
.
【解析】
(1)根据题意可得![]() ,由此求得椭圆方程。
,由此求得椭圆方程。
(2)设![]() ,利用点差法求出线段
,利用点差法求出线段![]() 中点
中点![]() 的轨迹方程。
的轨迹方程。
(3)设直线![]() 的方程为:
的方程为:![]() ,直线
,直线![]() 的方程为:
的方程为:![]() ,联立求得
,联立求得![]() ,由此证明点
,由此证明点![]() 的横坐标为定值。
的横坐标为定值。
(1)![]() 椭圆
椭圆![]() 两顶点
两顶点![]() ,短轴长为
,短轴长为![]() ,焦距为
,焦距为![]() ,
,
![]() ,解得
,解得![]()
![]() 椭圆方程为:
椭圆方程为:![]() .
.
(2)设![]() ,
,
则![]() ①,
①,![]() ②,
②,
则①![]() ②得
②得![]()
![]() ,
,
![]() ,
,
![]()
即![]() .
.
![]() 线段
线段![]() 中点
中点![]() 的轨迹方程为:
的轨迹方程为:![]() .
.
(3)证明:设直线![]() 的方程为:
的方程为:![]() ,
,
直线![]() 的方程为:
的方程为:![]() ,
,
两式联立可得:![]()
由①![]() ②得
②得![]()
![]()
即![]() ③,
③,
又![]() 三点共线,则
三点共线,则![]() ④,
④,
②代入③得![]()
把③④代入⑤整理得![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
【题目】某学习小组在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是小组成员在3月份的31天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 3月2日 | 3月8日 | 3月15日 | 3月22日 | 3月28日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 14 |
(1)在这个学习小组中负责统计数据的那位同学为了减少计算量,他从这5天中去掉了3月2日与3月28日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)若由线性回归方程得到的估计数据与所去掉的试验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
(参考公式: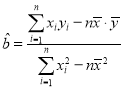 ,
,![]() )(参考数据:
)(参考数据:![]() ,
,![]() )
)