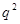题目内容
设ξ是一个离散型随机变量,其分布列如下表,则q=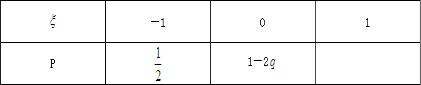
分析:因为随机变量的概率非负不大于1,且随机变量取遍所有可能值时相应的概率之和等于1,根据这样的特点列出方程和不等式,解方程得到结果,代入不等式检验,把不合题意的舍去.
解答:解:因为随机变量的概率非负
且随机变量取遍所有可能值时相应的概率之和等于1,
+1-2q+q2=1 ①
0≤1-2q≤1 ②
q2≤1③
∴解一元二次方程得q=1±
,
而1+
代入②③不合题意,舍去,
故答案为:1-
.
且随机变量取遍所有可能值时相应的概率之和等于1,
| 1 |
| 2 |
0≤1-2q≤1 ②
q2≤1③
∴解一元二次方程得q=1±
| ||
| 2 |
而1+
| ||
| 2 |
故答案为:1-
| ||
| 2 |
点评:本题主要考查分布列的简单应用,通过解方程组得到要求的变量,这与求变量的分布列是一个相反的过程,但是两者都要用到分布列的性质.

练习册系列答案
相关题目
设X是一个离散型随机变量,其分布列如图,则q等于( )
| x | -1 | 0 | 1 |
| P | 0.5 | 1-2q | q2 |
| A、1 | ||||
B、1±
| ||||
C、1-
| ||||
D、1+
|