题目内容
(1)如果两个实数u<v,求证:2u<
<2v.
(2)定义 设函数F(x)和f(x)都在区间I上有定义,若对I的任意子区间[u,v],总有[u,v]上的p和q,使有不等式f(p)≤
≤f(q)成立,则称F(x)是f(x)在区间I上的甲函数,f(x)是F(x)在区间I上的乙函数.
请根据乙函数定义证明:在(0,+∞)上,函数g(x)=
是f(x)=
的乙函数.
| v2-u2 |
| v-u |
(2)定义 设函数F(x)和f(x)都在区间I上有定义,若对I的任意子区间[u,v],总有[u,v]上的p和q,使有不等式f(p)≤
| F(u)-F(v) |
| u-v |
请根据乙函数定义证明:在(0,+∞)上,函数g(x)=
| 1 | ||
2
|
| x |
分析:(1)由u<v有 2u<u+v<2v,结合u+v═
,可证;
(2)根据f(x)是F(x)在区间I上的乙函数的定义,只需证:g(v)=
≤
≤
=g(u).
| v2-u2 |
| v-u |
(2)根据f(x)是F(x)在区间I上的乙函数的定义,只需证:g(v)=
| 1 | ||
2
|
| f(v)-f(u) |
| v-u |
| 1 | ||
2
|
解答:解:(1)证:由u<v有 2u<u+v<2v. 即 2u<
<2v
(2 )证明:对0<u<v有
=
=
不等式g(v)=
≤
≤
=g(u)
表明,g(x)=
是f(x)=
的乙函数.
| v2-u2 |
| v-u |
(2 )证明:对0<u<v有
| f(v)-f(u) |
| v-u |
| ||||
| v-u |
| 1 | ||||
|
不等式g(v)=
| 1 | ||
2
|
| 1 | ||||
|
| 1 | ||
2
|
表明,g(x)=
| 1 | ||
2
|
| x |
点评:本题以函数为载体,考查新定义,考查新函数的运用,关键是理解新定义.

练习册系列答案
相关题目
 (2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥
(2009•金山区二模)(1)设u、v为实数,证明:u2+v2≥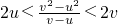 .
.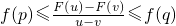 成立,则称F(x)是f(x)在区间I上的甲函数,f(x)是F(x)在区间I上的乙函数.
成立,则称F(x)是f(x)在区间I上的甲函数,f(x)是F(x)在区间I上的乙函数.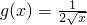 是
是 的乙函数.
的乙函数.