题目内容
已知函数y=4sin(| 1 |
| 3 |
| π |
| 6 |
| π |
| 2 |
| 11π |
| 2 |
分析:五点法作图
解答:请在列表中完成取点:

请在给定的直角坐标系中作出简图:
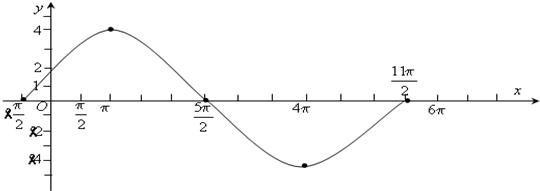 (8分)
(8分)
说明由y=sinx(x∈[0,2π])如何变换得到:
①将y=sinx(x∈[0,2π])图象中每一点向左平移
个单位,
得到y=sin(x+
);
②将y=sin(x+
)图象上每一个点的横坐标伸长为原来的3倍(纵标不变),
得到y=sin(
x+
);
③将y=sin(
x+
)图象上每一个点的纵标变为原来的4倍(横标不变),
得到y=4sin(
x+
).(12分)

请在给定的直角坐标系中作出简图:
 (8分)
(8分)说明由y=sinx(x∈[0,2π])如何变换得到:
①将y=sinx(x∈[0,2π])图象中每一点向左平移
| π |
| 6 |
得到y=sin(x+
| π |
| 6 |
②将y=sin(x+
| π |
| 6 |
得到y=sin(
| 1 |
| 3 |
| π |
| 6 |
③将y=sin(
| 1 |
| 3 |
| π |
| 6 |
得到y=4sin(
| 1 |
| 3 |
| π |
| 6 |
点评:此题是正弦型函数作图的典例,有较强的代表性,也是基础知识,属于熟练掌握的内容

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 x+
x+ ),其中x∈[-
),其中x∈[- ,
, ].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到.
].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到. x+
x+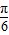 ),其中x∈[-
),其中x∈[-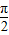 ,
, ].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到.
].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到.