题目内容
已知函数y=4sin(2x+
)(x∈[0,
])的图象与直线y=m有三个交点的横坐标分别为x1,x2,x3(x1<x2<x3),那么x1+2x2+x3的值是( )
| π |
| 6 |
| 7π |
| 6 |
分析:通过正弦函数的对称轴方程,求出函数的对称轴方程分别为x=
和x=
,由题意可得x1+x2=2×
,x2+x3 =2×
,从而求出x1+2x2+x3的值.
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
解答:解:函数y=4sin(2x+
)(x∈[0,
])的图象取得最值有2个x值,分别为
x=
和x=
,由正弦函数图象的对称性可得x1+x2=2×
=
,x2+x3 =2×
=
.
故x1+2x2+x3=x1+x2+x2+x3=
+
=
,
故选:C.
| π |
| 6 |
| 7π |
| 6 |
x=
| π |
| 6 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| 4π |
| 3 |
故x1+2x2+x3=x1+x2+x2+x3=
| π |
| 3 |
| 4π |
| 3 |
| 5π |
| 3 |
故选:C.
点评:本题主要考查三角函数y=Asin(ωx+∅)的对称性,考查计算能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
 x+
x+ ),其中x∈[-
),其中x∈[- ,
, ].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到.
].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到. x+
x+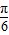 ),其中x∈[-
),其中x∈[-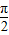 ,
, ].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到.
].先用“五点法“画出函数的简图,然后说明由y=sinx(x∈[0,2π]可经怎样变换得到.