题目内容
1．比较下列代数式的大小（1）-x2+x与-x+6；
（2）x2+2x与x2+x-2．
分析 作差，再配方，就可比较大小．
解答 解：（1）-x2+x+x-6=-x2+2x-6=-（x2-2x+1）-5=-（x-1）2-5＜0，
∴-x2+x＜-x+6；
（2）x2+2x-x2-x+2=x+2，当x≥-2时，x2+2x≥x2+x-2，当x＜-2时，x2+2x＜x2+x-2．
点评 本题考查利用作差法比较大小，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．已知函数f（x）=$\frac{cx}{2x+3}$，x≠-$\frac{3}{2}$，且对于不等于-$\frac{3}{2}$的任何实数x，满足f[f（x）]=x，则实数c的值为（ ）
| A． | -3 | B． | -2 | C． | 2 | D． | 3 |
12．
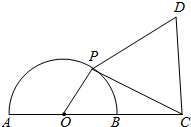如图，已知半圆的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上一个动点，以DC为边作等边三角形PCD，且点D与圆心分别在PC的两侧，则四边形OPDC面积的最大值为（ ）
如图，已知半圆的直径AB=2，点C在AB的延长线上，BC=1，点P为半圆上一个动点，以DC为边作等边三角形PCD，且点D与圆心分别在PC的两侧，则四边形OPDC面积的最大值为（ ）| A． | 2 | B． | $\frac{5\sqrt{3}}{4}$-2 | C． | $\frac{5\sqrt{3}}{4}$ | D． | 2+$\frac{5\sqrt{3}}{4}$ |