题目内容
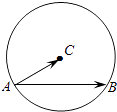
【题目】如图,定圆C的半径为4,A为圆C上的一个定点,B为圆C上的动点,若点A,B,C不共线,且 ![]() 对任意的t∈(0,+∞)恒成立,则
对任意的t∈(0,+∞)恒成立,则 ![]() = .
= . 
【答案】16
【解析】解:∵ ![]() =|
=| ![]() |,∴
|,∴ ![]() ﹣2t
﹣2t ![]() +t2
+t2 ![]() ≥
≥ ![]() ﹣2
﹣2 ![]() +
+ ![]() ,∴8t2﹣t
,∴8t2﹣t ![]() +
+ ![]() ﹣8≥0在(0,+∞)上恒成立,
﹣8≥0在(0,+∞)上恒成立,
△=( ![]() )2﹣32(
)2﹣32( ![]() ﹣8)=(
﹣8)=( ![]() ﹣16)2≥0,
﹣16)2≥0,
若△=0, ![]() =16,则8t2﹣t
=16,则8t2﹣t ![]() +
+ ![]() ﹣8≥0在R上恒成立,符合题意;
﹣8≥0在R上恒成立,符合题意;
若△>0, ![]() ≠16,则8t2﹣t
≠16,则8t2﹣t ![]() +
+ ![]() ﹣8=0的最大解x0=
﹣8=0的最大解x0= ![]() ≤0.
≤0.
当 ![]() >16时,x0=
>16时,x0= ![]() ≤0,解得
≤0,解得 ![]() =8(舍去).
=8(舍去).
当 ![]() <16时,x0=1,不符合题意.
<16时,x0=1,不符合题意.
综上, ![]() =16.
=16.
故答案为16.
对 ![]() =|
=| ![]() |两边平方,得到关于t的二次不等式在(0,+∞)上恒成立,讨论判别式和根的范围列出不等式解出.
|两边平方,得到关于t的二次不等式在(0,+∞)上恒成立,讨论判别式和根的范围列出不等式解出.

练习册系列答案
相关题目
【题目】某成衣批发店为了对一款成衣进行合理定价,将该款成衣按事先拟定的价格进行试销,得到了如下数据:
批发单价x(元) | 80 | 82 | 84 | 86 | 88 | 90 |
销售量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() ,其中
,其中 ![]()
(2)预测批发单价定为85元时,销售量大概是多少件?
(3)假设在今后的销售中,销售量与批发单价仍然服从(1)中的关系,且该款成衣的成本价为40元/件,为使该成衣批发店在该款成衣上获得更大利润,该款成衣单价大约定为多少元?