题目内容
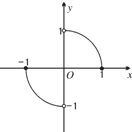函数y=f（x）的图象是以原点为圆心，1为半径的两段圆弧，则不等式f（x）＞f（-x）+x的解集为（ ）分析：由函数的图象可知，函数y=f（x）是奇函数，则不等式f（x）＞f（-x）+x等价为f（x）＞-f（x）+x，即2f（x）＞x成立．解不等式即可．
解答：解：函数的图象可知，函数y=f（x）是奇函数，则f（-x）=-f（x），所以不等式f（x）＞f（-x）+x等价为f（x）＞-f（x）+x，
即f（x）＞
．
对应圆的方程为x2+y2=1，联立直线y=
得，x=±
，所以由图象可知不等式f（x）＞f（-x）+x的解集为[-1，-
）∪（0，
）．
故选C．
即f（x）＞
| x |
| 2 |
对应圆的方程为x2+y2=1，联立直线y=
| x |
| 2 |
2
| ||
| 5 |
2
| ||
| 5 |
2
| ||
| 5 |
故选C．
点评：本题主要考查函数奇偶性的应用，利用图象的对称性判断函数是奇函数是解决本题的关键，然后利用直线与圆的方程解方程即可．
练习册系列答案
相关题目
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示，给出关于f（x）的下列命题：