题目内容
已知函数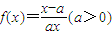
(1)判断并证明y=f(x)在x∈(0,+∞)上的单调性;
(2)若存在x,使f(x)=x,则称x为函数f(x)的不动点,现已知该函数有且仅有一个不动点,求a的值,并求出不动点x;
(3)若f(x)<2x在x∈(0,+∞)上恒成立,求a的取值范围.
【答案】分析:(1)先对函数的表达式进行化简,然后根据函数单调性的定义进行判断.
(2)令 转化为二次函数,根据该函数有且仅有一个不动点,令判别式等于0即可求出a的值.
转化为二次函数,根据该函数有且仅有一个不动点,令判别式等于0即可求出a的值.
(3)将函数解析式代入f(x)<2x中,整理为 ,在根据基本不等式的知识求出
,在根据基本不等式的知识求出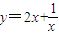 的最小值,令此最小值大于
的最小值,令此最小值大于 ,即可求出a的范围.
,即可求出a的范围.
解答:解:(1)
对任意的x1,x2∈(0,+∞)且x1>x2
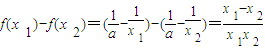
∵x1>x2>0
∴x1-x2>0,x1x2>0
∴f(x1)-f(x2)>0,函数y=f(x)在x∈(0,+∞)上单调递增.
(2)解:令 ,
,
令 (负值舍去)
(负值舍去)
将 代入ax2-x+a=0得
代入ax2-x+a=0得
(3)∵f(x)<2x
∴
∵x>0
∴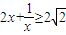 (等号成立当
(等号成立当 )
)
∴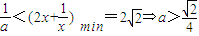
∴a的取值范围是
点评:本题主要考查函数单调性的定义和基本不等式的应用.考查计算能力和综合运用能力.
(2)令
 转化为二次函数,根据该函数有且仅有一个不动点,令判别式等于0即可求出a的值.
转化为二次函数,根据该函数有且仅有一个不动点,令判别式等于0即可求出a的值.(3)将函数解析式代入f(x)<2x中,整理为
 ,在根据基本不等式的知识求出
,在根据基本不等式的知识求出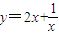 的最小值,令此最小值大于
的最小值,令此最小值大于 ,即可求出a的范围.
,即可求出a的范围.解答:解:(1)

对任意的x1,x2∈(0,+∞)且x1>x2
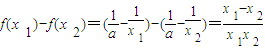
∵x1>x2>0
∴x1-x2>0,x1x2>0
∴f(x1)-f(x2)>0,函数y=f(x)在x∈(0,+∞)上单调递增.
(2)解:令
 ,
,令
 (负值舍去)
(负值舍去)将
 代入ax2-x+a=0得
代入ax2-x+a=0得
(3)∵f(x)<2x
∴

∵x>0
∴
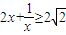 (等号成立当
(等号成立当 )
)∴
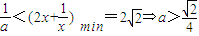
∴a的取值范围是

点评:本题主要考查函数单调性的定义和基本不等式的应用.考查计算能力和综合运用能力.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目

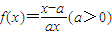
 .
.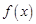 的奇偶性;
的奇偶性;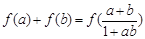 ;
; ,
, ,求
,求 ,
,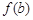 的值.
的值.