题目内容
(1)若对于任意的n∈N*,总有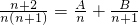 成立,求常数A,B的值;
成立,求常数A,B的值;
(2)在数列{an}中, ,
,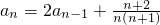 (n≥2,n∈N*),求通项an;
(n≥2,n∈N*),求通项an;
(3)在(2)题的条件下,设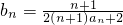 ,从数列{bn}中依次取出第k1项,第k2项,…第kn项,按原来的顺序组成新的数列{cn},其中
,从数列{bn}中依次取出第k1项,第k2项,…第kn项,按原来的顺序组成新的数列{cn},其中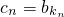 ,其中k1=m,kn+1-kn=r∈N*.试问是否存在正整数m,r使
,其中k1=m,kn+1-kn=r∈N*.试问是否存在正整数m,r使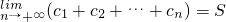 且
且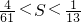 成立?若存在,求正整数m,r的值;不存在,说明理由.
成立?若存在,求正整数m,r的值;不存在,说明理由.
解:(1)由题设得A(n+1)+Bn=n+2即(A+B)n+A=n+2恒成立,
所以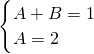 A=2,B=-1.(4分)
A=2,B=-1.(4分)
(2)由题设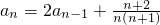 (n≥2)又
(n≥2)又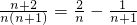 得,
得,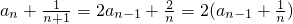 ,且
,且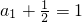 ,
,
即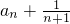 是首项为1,公比为2的等比数列,(8分)
是首项为1,公比为2的等比数列,(8分)
所以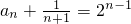 .即
.即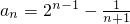 为所求.(9分)
为所求.(9分)
(3)假设存在正整数m,r满足题设,由(2)知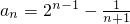
显然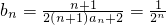 ,
,
又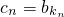 得
得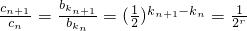 ,
,
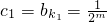 即{cn}是以
即{cn}是以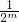 为首项,
为首项, 为公比的等比数列.(11分)
为公比的等比数列.(11分)
于是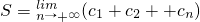 =
=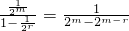 ,(12分)
,(12分)
由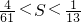 得
得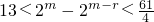 ,m,r∈N*,
,m,r∈N*,
所以2m-2m-r=14或15,(14分)
当2m-2m-r=14时,m=4,r=3;
当2m-2m-r=15时,m=4,r=4;
综上,存在正整数m,r满足题设,m=4,r=3或m=4,r=4.(16分)
分析:(1)由题设得(A+B)n+A=n+2恒成立,所以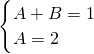 A=2,B=-1.
A=2,B=-1.
(2)由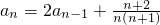 (n≥2)和
(n≥2)和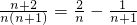 知,
知,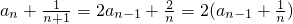 ,且
,且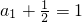 ,由此能推导出
,由此能推导出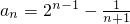 .
.
(3)假设存在正整数m,r满足题设,由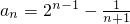 ,
,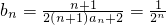 ,又
,又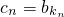 得
得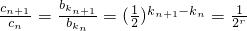 ,
,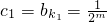 .于是
.于是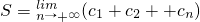 =
=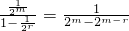 ,由此能推导出存在正整数m,r满足题设,m=4,r=3或m=4,r=4.
,由此能推导出存在正整数m,r满足题设,m=4,r=3或m=4,r=4.
点评:本题考查数列中参数的求法、等差数列的通项公式和以极限为载体考查数列性质的综合运用,解题时要认真审题,仔细解答.
所以
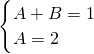 A=2,B=-1.(4分)
A=2,B=-1.(4分)(2)由题设
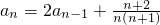 (n≥2)又
(n≥2)又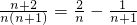 得,
得,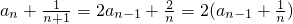 ,且
,且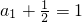 ,
,即
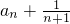 是首项为1,公比为2的等比数列,(8分)
是首项为1,公比为2的等比数列,(8分)所以
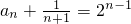 .即
.即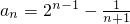 为所求.(9分)
为所求.(9分)(3)假设存在正整数m,r满足题设,由(2)知
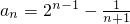
显然
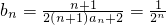 ,
,又
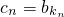 得
得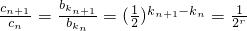 ,
,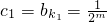 即{cn}是以
即{cn}是以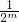 为首项,
为首项, 为公比的等比数列.(11分)
为公比的等比数列.(11分)于是
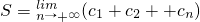 =
=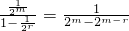 ,(12分)
,(12分)由
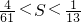 得
得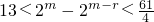 ,m,r∈N*,
,m,r∈N*,所以2m-2m-r=14或15,(14分)
当2m-2m-r=14时,m=4,r=3;
当2m-2m-r=15时,m=4,r=4;
综上,存在正整数m,r满足题设,m=4,r=3或m=4,r=4.(16分)
分析:(1)由题设得(A+B)n+A=n+2恒成立,所以
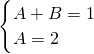 A=2,B=-1.
A=2,B=-1.(2)由
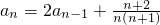 (n≥2)和
(n≥2)和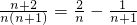 知,
知,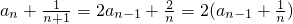 ,且
,且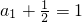 ,由此能推导出
,由此能推导出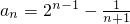 .
.(3)假设存在正整数m,r满足题设,由
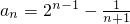 ,
,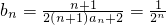 ,又
,又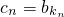 得
得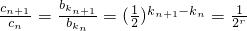 ,
,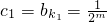 .于是
.于是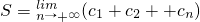 =
=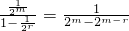 ,由此能推导出存在正整数m,r满足题设,m=4,r=3或m=4,r=4.
,由此能推导出存在正整数m,r满足题设,m=4,r=3或m=4,r=4.点评:本题考查数列中参数的求法、等差数列的通项公式和以极限为载体考查数列性质的综合运用,解题时要认真审题,仔细解答.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
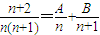 成立,求常数A,B的值;
成立,求常数A,B的值;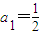 ,
,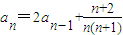 (n≥2,n∈N*),求通项an;
(n≥2,n∈N*),求通项an;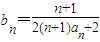 ,从数列{bn}中依次取出第k1项,第k2项,…第kn项,按原来的顺序组成新的数列{cn},其中
,从数列{bn}中依次取出第k1项,第k2项,…第kn项,按原来的顺序组成新的数列{cn},其中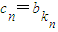 ,其中k1=m,kn+1-kn=r∈N*.试问是否存在正整数m,r使
,其中k1=m,kn+1-kn=r∈N*.试问是否存在正整数m,r使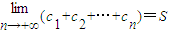 且
且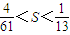 成立?若存在,求正整数m,r的值;不存在,说明理由.
成立?若存在,求正整数m,r的值;不存在,说明理由.