题目内容
(本小题满分12分)
在锐角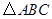 中,内角
中,内角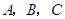 对边的边长分别是
对边的边长分别是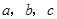 ,且
,且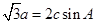
(1)求角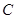 的值;
的值;
(2)若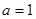 ,
,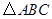 的面积为
的面积为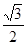
 ,求
,求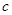 的值。
的值。
在锐角
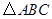 中,内角
中,内角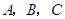 对边的边长分别是
对边的边长分别是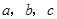 ,且
,且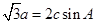
(1)求角
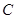 的值;
的值;(2)若
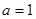 ,
,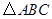 的面积为
的面积为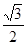
 ,求
,求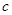 的值。
的值。(1),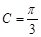 。(Ⅱ)
。(Ⅱ)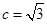 。
。
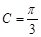 。(Ⅱ)
。(Ⅱ)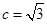 。
。试题分析:(Ⅰ)由
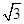 a=2csinA及正弦定理得,
a=2csinA及正弦定理得,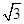 sinA=2sinCsinA,得sinC=
sinA=2sinCsinA,得sinC= 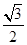 ,从而得到C值.
,从而得到C值.(Ⅱ)由面积公式得S=
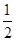 absinC=
absinC= 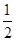 ×3×bsin
×3×bsin 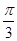 =
= 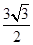 ,解方程求得边长b.
,解方程求得边长b.解:(1)由
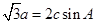 及正弦定理得,
及正弦定理得,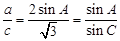 ,…………………….4分
,…………………….4分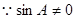
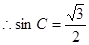 ,
,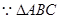 是锐角三角形,
是锐角三角形, 。 ………6分
。 ………6分(Ⅱ)由面积公式得,
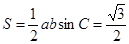 ,
,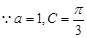 ,
,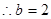 , ……….9分
, ……….9分由余弦定理得,
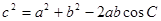
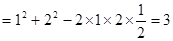 ,,
,,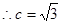 。……….12分考点:
。……….12分考点:点评:解决该试题的关键是由
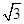 a=2csinA及正弦定理得,
a=2csinA及正弦定理得,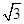 sinA=2sinCsinA,并由此得到角C的正弦值。
sinA=2sinCsinA,并由此得到角C的正弦值。
练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
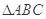 中,
中,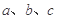 分别为内角
分别为内角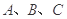 所对的边,且
所对的边,且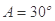 .现给出三个条件:①
.现给出三个条件:① ; ②
; ②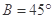 ;③
;③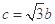 .试从中选出两个可以确定
.试从中选出两个可以确定 中,
中, ,若以
,若以 为焦点的椭圆经过点
为焦点的椭圆经过点 ,则该椭圆的离心率
,则该椭圆的离心率 ( )
( )



 中,
中, ,
, ,则角
,则角 等于( )
等于( )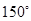



 的三边长分别为
的三边长分别为 ,若
,若 ,则A等于( )
,则A等于( )



 所对的分别是
所对的分别是 。已知
。已知 。(1)求
。(1)求 的值;
的值; 的值。
的值。 中,内角
中,内角 的对边分别为
的对边分别为 。已知
。已知 ,
, 。(1)求
。(1)求 ;(2)若
;(2)若 ,求△
,求△ 、
、 、
、 为
为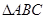 的三内角,且其对边分别为
的三内角,且其对边分别为 、
、 、
、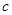 ,若
,若 .
. ,求
,求 是锐角,且满足
是锐角,且满足 ,则
,则 的值为( ).
的值为( ).


