题目内容
对于任意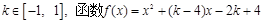
的值恒大于零，则x的取值范围是 .
【答案】
【解析】
试题分析：解：∵任意k∈[-1，，1]，，函数f（x）=x2+（k-4）x-2k+4＞0，恒成立，∴f（k）=k（x-2）+x2-4x+4＞0为一次函数，∴f(-1)>0,f(1)>0，∴-1（x-2）+x2-4x+4＞0，（x-2）+x2-4x+4＞0，解得x＜1或x＞3，故答案为（-∞，1）∪（3，+∞）．
考点：函数的单调性
点评：此题是一道常见的题型，把关于x的函数转化为关于k的函数，构造一次函数，因为一次函数是单调函数易于求解，最此类恒成立题要注意
练习册系列答案
相关题目
对于任意k∈[-1，1]，函数f（x）=x2+（k-4）x-2k+4的值恒大于零，则x的取值范围是（）
| A、x＜0 | B、x＞4 | C、x＜1或x＞3 | D、x＜1 |