题目内容
【题目】在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上异于
上异于![]() 的一点,光线从点
的一点,光线从点![]() 出发,经
出发,经![]() 反射后又回到原点
反射后又回到原点![]() ,光线
,光线![]() 经过
经过![]() 的重心.
的重心.
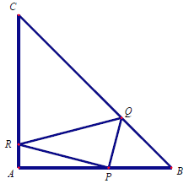
(1)建立适当的坐标系,请求![]() 的重心
的重心![]() 的坐标;
的坐标;
(2)求点![]() 的坐标;
的坐标;
(3)求![]() 的周长及面积.
的周长及面积.
【答案】(1)坐标系见解析,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]()
![]()
【解析】
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立直角坐标系,依次写出
轴建立直角坐标系,依次写出![]() 的坐标,由重心公式求得重心即可;
的坐标,由重心公式求得重心即可;
(2)由光的反射具有对称性,作![]() 关于
关于![]() 的对称点
的对称点![]() ,关于
,关于![]() 的对称点
的对称点![]() ,则
,则![]() 四点共线,设
四点共线,设![]() ,根据对称性可得
,根据对称性可得![]() ,
,![]() ,且
,且![]() 在直线
在直线![]() 上,解出
上,解出![]() 方程并将点
方程并将点![]() 坐标代入即可求得
坐标代入即可求得![]() ,进而得到
,进而得到![]() 的坐标;
的坐标;
(3)由(2), ![]() 的周长转化为
的周长转化为![]() 的长,利用割补法将
的长,利用割补法将![]() 的面积转化为
的面积转化为![]() 的面积与
的面积与![]() 的面积的差计算即可
的面积的差计算即可
(1)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立直角坐标系,则
轴建立直角坐标系,则![]() ,
,![]() ,
,![]() ,
,
所以根据重心公式可得重心![]() 为
为![]() ,即
,即![]()
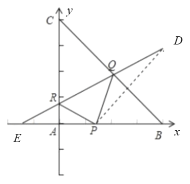
(2)作![]() 关于
关于![]() 的对称点
的对称点![]() ,关于
,关于![]() 的对称点
的对称点![]() ,由于光的反射原理,
,由于光的反射原理,![]() 四点共线,
四点共线,
因为![]() 过重心
过重心![]() ,所以
,所以![]() 过重心
过重心![]() ,
,
设![]() ,则
,则![]() ,
,
因为![]() ,
,![]() ,所以直线
,所以直线![]() 为:
为:![]() ,
,
设![]() ,则
,则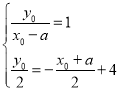 ,所以
,所以 ,即
,即![]()
则直线![]() 为
为![]() ,
,
由(1),代入点![]() ,即
,即![]() ,
,
所以![]() 或
或![]() ,
,
因为![]() 异于
异于![]() ,
,
所以点![]() 为
为![]()
(3)由(2),![]() ,
,![]() ,
,
由于对称性,则![]() 的周长为:
的周长为: ,
,
直线![]() 为
为 ,即
,即![]() ,
,
当![]() 时,
时,![]() ,则
,则![]()
联立![]() ,解得
,解得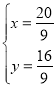 ,则
,则![]() ,
,
所以![]() 的面积为:
的面积为:![]()
![]()
![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目