题目内容
设双曲线的顶点是椭圆| x2 |
| 3 |
| y2 |
| 4 |
| 15 |
(1)求此双曲线的标准方程;
(2)求|AB|的长度.
分析:(1)利用条件双曲线的顶点是椭圆
+
=1的焦点,可以假双曲线的方程为y2-
=1,再结合条件OA⊥OB,可求双曲线的标准方程;(2)求|AB|的长度,利用两点间的距离公式求解.
| x2 |
| 3 |
| y2 |
| 4 |
| x2 |
| b2 |
解答:解:(1)椭圆
+
=1的焦点为(0,±1),依题意设双曲线的方程为y2-
=1,设A(x1,y1),B(x2,y2),则
x1=3y1-6,
x2=3y2-6,∴15x1x2=9y1y2-18(y1+y2)+36,
∴x1x2=
由 OA⊥OB,∴x1x2+y1y2=0,∴4y1y2-3(y1+y2)+6=0…①
由
,∴(15b2-9)y2+36y-(15b2+36)=0…②
∴y1+y2=
,y1y2=
,代入①中得b2=3∴双曲线的方程为y2-
=1
(2)将b2=3代入②式中,得4y2+4y-9=0,y1+y2=-1,y1y2=-
∴|AB|=
|y2-y1|=
•
)=4
| x2 |
| 3 |
| y2 |
| 4 |
| x2 |
| b2 |
| 15 |
| 15 |
∴x1x2=
| 3y1y2-6(y1+y2)+12 |
| 5 |
由 OA⊥OB,∴x1x2+y1y2=0,∴4y1y2-3(y1+y2)+6=0…①
由
|
∴y1+y2=
| 36 |
| 9-15b2 |
| 15b2+36 |
| 9-15b2 |
| x2 |
| 3 |
(2)将b2=3代入②式中,得4y2+4y-9=0,y1+y2=-1,y1y2=-
| 9 |
| 4 |
∴|AB|=
1+
|
1+
|
1-4×(-
|
点评:本题(1)问利用直线与曲线联立方程组,采用设而不求的方法,关键是设点;(2)问则在(1)问得基础上借助于两点间的距离公式求解.属于中档题.

练习册系列答案
相关题目
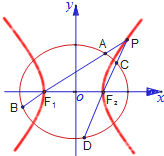 如图,已知椭圆
如图,已知椭圆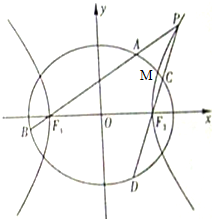 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆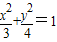 的焦点,该双曲线又与直线
的焦点,该双曲线又与直线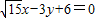 交于两点A、B且OA⊥OB(O为原点).
交于两点A、B且OA⊥OB(O为原点).