题目内容
(本题满分14分).
某校从高一年级学生中随机抽取60名学生,将其期中考试的数学成绩(均为整数)分成六段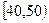 ,
,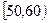 ,…,
,…,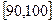 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)求分数在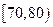 内的频率;
内的频率;
(2)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.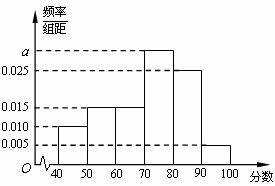
(14分).解:(1)分数在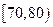 内的频率为:
内的频率为:
 .………
.……… 3分
3分
(2). 由题意, 分数段的人数为:
分数段的人数为: 人;………4分
人;………4分 分
分 数段的人数为:
数段的人数为: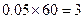 人; ………………5分
人; ………………5分
∵用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量 为6的样本,
为6的样本,
∴ 分数段抽
分数段抽 取
取 =5人, ……7分
=5人, ……7分 分数段抽取
分数段抽取 =1人, ……9分
=1人, ……9分
抽取 分数段5人,分别记为a,b,c,d,e;
分数段5人,分别记为a,b,c,d,e;
抽取 分数段抽取1人记为m. ………………10分
分数段抽取1人记为m. ………………10分
因为从样本中任取2人,其中恰有1人的分数不低于90分,
则另一人的分数一定是在 分数段,所以只需在分数段
分数段,所以只需在分数段 抽取的5人中确定1人.
抽取的5人中确定1人.
设“从样本中任取2人,其中恰有1人的分数不低于90分为”事件 , ………………11分
, ………………11分
则基本事件空间包含的基本事件有:(a,b ),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),(a,m),(b,m),(c,m),(d,m),(e,m)共
),(a,c),(a,d),(a,e),(b,c),(b,d),(b,e),(c,d),(c,e),(d,e),(a,m),(b,m),(c,m),(d,m),(e,m)共 15种.……12分
15种.……12分
事件 包含的基本事件有(a,m),(b,m),(c,m),(d,m),(e,m)共5种.………13分
包含的基本事件有(a,m),(b,m),(c,m),(d,m),(e,m)共5种.………13分
∴恰有1人的分数不低于90分的概率为 . ……………14分
. ……………14分
解析

某校为了解学生的学科学习兴趣,对初高中学生做了一个喜欢数学和喜欢语文的抽样调查,随机抽取了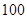 名学生,相关的数据如下表所示:
名学生,相关的数据如下表所示:
| | 数学 | 语文 | 总计 |
| 初中 | 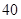 | 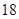 | 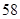 |
| 高中 | 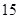 | 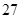 | 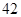 |
| 总计 | 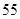 | 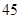 | 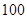 |
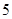 名,高中学生应该抽取几名?
名,高中学生应该抽取几名?(2) 在(1)中抽取的
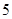 名学生中任取
名学生中任取 名,求恰有
名,求恰有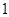 名初中学生的概率.
名初中学生的概率. 10分)某公司在过去几年内使用某种型号的灯管1000支,该公司对这些灯管的使用寿命
(单位:小时)进行了统计,统计结果如下表所示:
| 分组 |  |  |  | 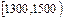 |  | 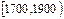 |  |
| 组数 | 48 | 121 | 208 | 223 | 193 | 165 | 42 |
| 频率 | | | | | | | |
(2) 根据上述统计结果,计算灯管使用寿命不足1500小时的频率;
(3) 该公司某办公室新安装了这种型号的灯管3支,若将上述频率作为概率,试求至少有2支灯管的使用寿命不足1500小时的概率

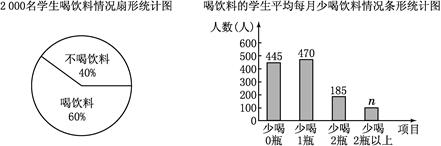
 希望工程?
希望工程? 个网站哪个更受欢迎?并说明理由。
个网站哪个更受欢迎?并说明理由。 
 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表: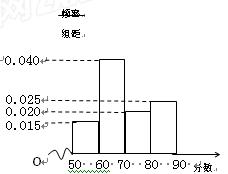
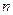 件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把
件,合格率为96%,在投放市场之前,决定对该产品进行最后检验,为了减少检验次数,科技人员采用打包的形式进行,即把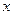 件打成一包,对这
件打成一包,对这 果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了
果检测仪器显示绿灯,说明该包产品均为合格品;如果检测仪器显示红灯,说明该包产品至少有一件不合格,须对该包产品一共检测了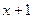 次
次 测这
测这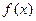 ;
;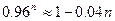 ,要使检测次数最少,则每包应放多少件产品?
,要使检测次数最少,则每包应放多少件产品?