题目内容
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠ABC=45°,AB=2,BC=2![]() ,SA=SB=
,SA=SB=![]() .
.
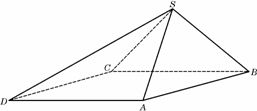
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.
答案:
解析:
解析:
|
解答:解法一: (Ⅰ)作 因为 又 由三垂线定理,得
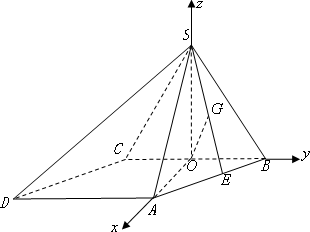
(Ⅱ)由(Ⅰ)知 故 连结 设 解得 设 所以,直线 解法二: (Ⅰ)作 因为 又 如下图,以 所以
(Ⅱ)取 连结 所以 所以,直线 |

练习册系列答案
相关题目
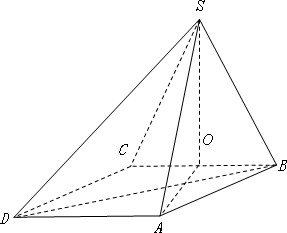
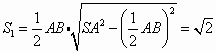 .
.
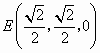 ,
,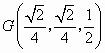 .
.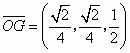 ,
,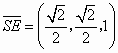 ,
,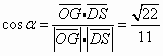 ,
,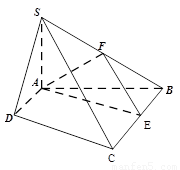
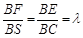 .(
.(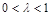 )
)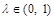 ,恒有SC∥平面AEF;
,恒有SC∥平面AEF;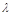 ,使得△AEF为直角三角形,若存在,求出所有符合条件的
,使得△AEF为直角三角形,若存在,求出所有符合条件的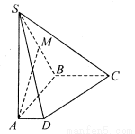
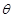 ,求sin
,求sin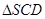 内及其边界上运动,并且总是保持PE
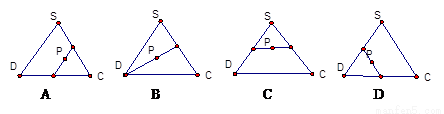
内及其边界上运动,并且总是保持PE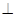 AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是(
).
AC.则动点P的轨迹与△SCD组成的相关图形最有可能的是(
).