题目内容
已知函数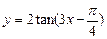 ,试研究该函数的性质.
,试研究该函数的性质.
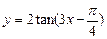 ,试研究该函数的性质.
,试研究该函数的性质.函数是非奇非偶函数.
令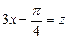 ,已知函数化为
,已知函数化为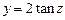 ,
,
由于函数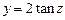 对不等于
对不等于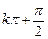
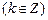 的实数
的实数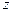 都有意义,且值域是R,
都有意义,且值域是R,
∴原函数的定义域是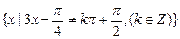 ,即
,即
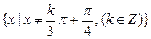 ,而值域是R;
,而值域是R;
又由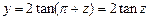 ,有
,有
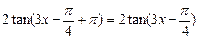 =
=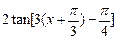 .
.
设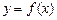 ,上式即是
,上式即是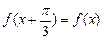 对定义域内的任意
对定义域内的任意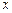 都成立,
都成立,
由周期函数的定义以及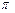 是正切函数的最小正周期,
是正切函数的最小正周期,
可知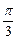 是函数
是函数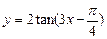 的最小正周期;
的最小正周期;
再由函数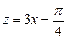 是关于
是关于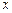 的单调增函数,
的单调增函数,
∴当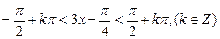 时,函数
时,函数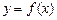 也单调递增,
也单调递增,
即函数的单调增区间是(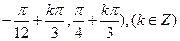 ;
;
∵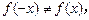
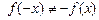 ,
,
∴函数是非奇非偶函数.
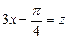 ,已知函数化为
,已知函数化为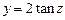 ,
,由于函数
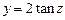 对不等于
对不等于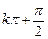
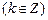 的实数
的实数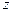 都有意义,且值域是R,
都有意义,且值域是R,∴原函数的定义域是
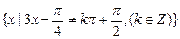 ,即
,即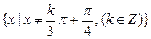 ,而值域是R;
,而值域是R;又由
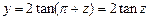 ,有
,有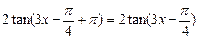 =
=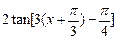 .
.设
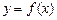 ,上式即是
,上式即是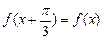 对定义域内的任意
对定义域内的任意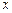 都成立,
都成立,由周期函数的定义以及
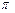 是正切函数的最小正周期,
是正切函数的最小正周期,可知
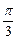 是函数
是函数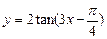 的最小正周期;
的最小正周期;再由函数
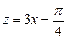 是关于
是关于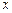 的单调增函数,
的单调增函数,∴当
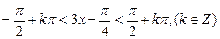 时,函数
时,函数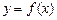 也单调递增,
也单调递增,即函数的单调增区间是(
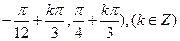 ;
;∵
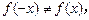
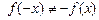 ,
,∴函数是非奇非偶函数.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
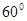 的方向,两船相距
的方向,两船相距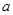 海里,乙船正在向北行驶,若甲船的速度是乙船的
海里,乙船正在向北行驶,若甲船的速度是乙船的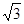 倍,甲船为了尽快追上乙船,应取北偏东
倍,甲船为了尽快追上乙船,应取北偏东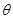 方向前进,则
方向前进,则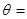
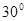
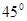
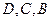 三点在地面同一直线上,
三点在地面同一直线上,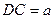 ,从
,从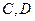 两点测得
两点测得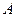 点仰角分别是
点仰角分别是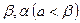 ,则
,则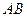 等于( ▲ )
等于( ▲ )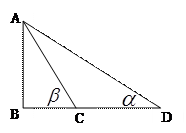
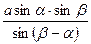 B.
B. 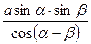 C
C 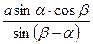 D .
D .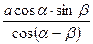
 方向走,当乙走了2千米到达B点时,两人距离恰好为
方向走,当乙走了2千米到达B点时,两人距离恰好为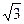 千米,那么这时甲走的距离是
千米,那么这时甲走的距离是 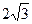 千米
千米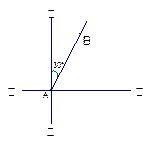
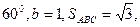 则
则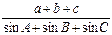 =" " ____。
=" " ____。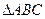 中,角
中,角 所对的边分别是
所对的边分别是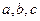 ,若
,若
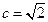 ,求
,求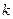 的值.
的值.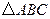 中,
中,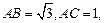
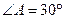 ,则
,则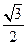
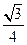

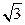
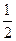
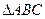 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为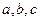 ,若
,若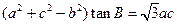 ,则角B的值为 .
,则角B的值为 .