题目内容
如图，AB是⊙O的弦，C是AB的三等分点，连接OC并延长交⊙O于点D．若OC=3，CD=2，则圆心O到弦AB的距离是（ ）分析：利用圆的相交弦定理和垂径定理、勾股定理即可得出．
解答：解：如图所示，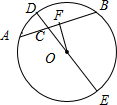
设AC=x，则BC=2x．
由相交弦定理可得：AC×BC=DC×CE，
∴2x2=2×（2+3+3），即x2=8，x=2
，∴AB=3x=6
．
过点O作OF⊥AB，垂直为F，则AF=FB=3
．
∴CF=
x-x=
x=
，
在Rt△OCF中，OF=
=
．
故选C．
设AC=x，则BC=2x．
由相交弦定理可得：AC×BC=DC×CE，
∴2x2=2×（2+3+3），即x2=8，x=2
| 2 |
| 2 |
过点O作OF⊥AB，垂直为F，则AF=FB=3
| 2 |
∴CF=
| 3 |
| 2 |
| 1 |
| 2 |
| 2 |
在Rt△OCF中，OF=
32-(
|
| 7 |
故选C．
点评：熟练掌握圆的相交弦定理和垂径定理、勾股定理是解题的关键．
练习册系列答案
相关题目
22、如图，AB是⊙O的弦，C、F是⊙O上的点，OC垂直于弦AB，过F点作⊙O的切线交AB的延长线于D，连接CF交AB于E点．
已知：如图，AB是⊙O的弦，点C在 
如图，AB是⊙O的弦，C、F是⊙O上的点，OC垂直于弦AB，过F点作⊙O的切线交AB的延长线于D，连接CF交AB于E点．