题目内容
为了了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，没得身高频数分布表如下表1、表2．表1：男生身高频数分布表
| 身高（cm） | [160，165） | [165，170） | [170，175） | [175，180） | [180，185） | [185，190） |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高（cm） | [150，155） | [155，160） | [160，165） | [165，170） | [170，175） | [175，180） |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
（Ⅱ）估计该校学生身高（单位：cm）在[165，180）的概率；
（Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望．
分析：（I）求出样本中男生的人数，除以分层抽样的比例，求出全校的男生人数．
（II）求出样本中身高在[165，180）男生的人数加上女生的人数，除以样本容量求出频率．
（III）写出随机变量可取得值，随机变量ξ服从超几何分布；利用古概型的概率公式求出随机变量取每一个值的概率值，列出分布列，利用随机变量的期望公式求出期望．
（II）求出样本中身高在[165，180）男生的人数加上女生的人数，除以样本容量求出频率．
（III）写出随机变量可取得值，随机变量ξ服从超几何分布；利用古概型的概率公式求出随机变量取每一个值的概率值，列出分布列，利用随机变量的期望公式求出期望．
解答：解：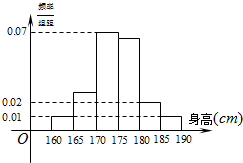
（Ⅰ）样本中男生人数为2+5+14+13+4+2=40，由分层抽样比例为10%可得全校男生人数为400
频率分布直方图如图示
（Ⅱ）由表1、表2可知，样本中身高在[165，180）
的学生人数为：5+14+13+6+3+1=42，样本容量
为70，所以样本中学生身高在[165，180）的频率f=
=
（Ⅲ）依题意知ξ的可能值为：1，2，3
∵P(ξ=1)=
=
，P(ξ=2)=
=
，P(ξ=3)=
=
∴ξ的分布列为：
∴ξ的数学期望Eξ=1×
+2×
+3×
=2
（Ⅰ）样本中男生人数为2+5+14+13+4+2=40，由分层抽样比例为10%可得全校男生人数为400频率分布直方图如图示
（Ⅱ）由表1、表2可知，样本中身高在[165，180）
的学生人数为：5+14+13+6+3+1=42，样本容量
为70，所以样本中学生身高在[165，180）的频率f=
| 42 |
| 70 |
| 3 |
| 5 |
∵P(ξ=1)=
| ||
|
| 1 |
| 5 |
| ||||
|
| 3 |
| 5 |
| ||
|
| 1 |
| 5 |
| ξ | 1 | 2 | 3 | ||||||
| P |
|
|
|
∴ξ的数学期望Eξ=1×
| 1 |
| 5 |
| 3 |
| 5 |
| 1 |
| 5 |
点评：本题考查频率等于频数除以样本容量、考查求随机变量的分布列的步骤及求随机变量的期望公式．
练习册系列答案
巧学巧练系列答案
相关题目
为了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，测得身高频数分布表如下表1、表2．
表1：男生身高频数分布表
表2：女生身高频数分布表
（1）求该校男生的人数并完成下面频率分布直方图；
（2）估计该校学生身高在[165：180）cm的概率；
（3）从样本中身高在[180：190）cm之间的男生中任选2人，求至少有1人身高在[185：190）cm之间的概率．
表1：男生身高频数分布表
| 身高（cm） | [160，165） | [165，170） | [170，175） | [175，180） | [180，185） | [185，190） |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高（cm） | [150，155） | [155，160） | [160，165） | [165，170） | [170，175） | [175，180） |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
（2）估计该校学生身高在[165：180）cm的概率；
（3）从样本中身高在[180：190）cm之间的男生中任选2人，求至少有1人身高在[185：190）cm之间的概率．
为了了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，没得身高频数分布表如下表1、表2．
表1：男生身高频数分布表
表2：女生身高频数分布表
（Ⅰ）求该校男生的人数并画出其频率分布直方图；
（Ⅱ）估计该校学生身高（单位：cm）在[165，180）的概率；
（Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望．
表1：男生身高频数分布表
| 身高（cm） | [160，165） | [165，170） | [170，175） | [175，180） | [180，185） | [185，190） |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高（cm） | [150，155） | [155，160） | [160，165） | [165，170） | [170，175） | [175，180） |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
（Ⅱ）估计该校学生身高（单位：cm）在[165，180）的概率；
（Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望．
为了了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，没得身高频数分布表如下表1、表2．
表1：男生身高频数分布表
表2：女生身高频数分布表
（Ⅰ）求该校男生的人数并画出其频率分布直方图；
（Ⅱ）估计该校学生身高（单位：cm）在[165，180）的概率；
（Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望．
表1：男生身高频数分布表
| 身高（cm） | [160，165） | [165，170） | [170，175） | [175，180） | [180，185） | [185，190） |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高（cm） | [150，155） | [155，160） | [160，165） | [165，170） | [170，175） | [175，180） |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
（Ⅱ）估计该校学生身高（单位：cm）在[165，180）的概率；
（Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望．
为了了解高中一年级学生身高情况，某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查，没得身高频数分布表如下表1、表2．
表1：男生身高频数分布表
表2：女生身高频数分布表
（Ⅰ）求该校男生的人数并画出其频率分布直方图；
（Ⅱ）估计该校学生身高（单位：cm）在[165，180）的概率；
（Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望．
表1：男生身高频数分布表
| 身高（cm） | [160，165） | [165，170） | [170，175） | [175，180） | [180，185） | [185，190） |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高（cm） | [150，155） | [155，160） | [160，165） | [165，170） | [170，175） | [175，180） |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
（Ⅱ）估计该校学生身高（单位：cm）在[165，180）的概率；
（Ⅲ）在男生样本中，从身高（单位：cm）在[180，190）的男生中任选3人，设ξ表示所选3人中身高（单位：cm）在[180，185）的人数，求ξ的分布列和数学期望．