题目内容
为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.表1:男生身高频数分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(2)估计该校学生身高在[165:180)cm的概率;
(3)从样本中身高在[180:190)cm之间的男生中任选2人,求至少有1人身高在[185:190)cm之间的概率.
(2)根据表1、表2知,样本中身高在165:180cm的学生人数,从而得到样本容量,根据频率=
| 频数 |
| 样本容量 |
(3)样本中身高在180:185cm之间的男生有4人,在样本中身高在180:190cm之间的男生中任选2人得所有可能结果数为15,而至少有1人身高在185:190cm之间的可能结果数为9,根据该古典概型的概率公式即可求出所求.
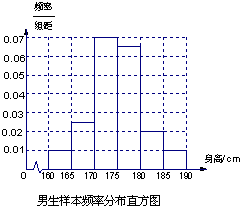 解:(1)样本中男生人数为40,
解:(1)样本中男生人数为40,由分层抽样比例为10%可得全校男生人数为400.(2分)
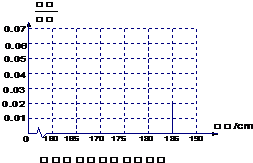
频率分布直方图如右图示:(4分)
(2)由表1、表2知,样本中身高在165:180cm
的学生人数为:5+14+13+6+3+1=42,样本容量为70,所以样本中学生身高在165:180cm
的频率f=
| 42 |
| 70 |
| 3 |
| 5 |
故由f估计该校学生身高在165:180cm
的概率p=
| 3 |
| 5 |
(3)样本中身高在180:185cm之间的男生有4人,设其编号为①②③④样本中身高在180:190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:
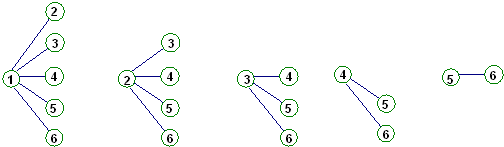
故从样本中身高在180~190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185~190cm之间的可能结果数为9,因此,所求概率p=
| 9 |
| 15 |
| 3 |
| 5 |

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案为了解高中一年级学生身高情况,某校按10%的比例对全校700名高中一年级学生按性别进行抽样检查,测得身高频数分布表如下表1、表2.
表1:男生身高频数分布表
|
身高(cm) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
[180,185) |
[185,190) |
|
频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2:女生身高频数分布表
|
身高(cm) |
[150,155) |
[155,160) |
[160,165) |
[165,170) |
[170,175) |
[175,180) |
|
频数 |
1 |
7 |
12 |
6 |
3 |
1 |
(I)求该校男生的人数并完成下面频率分布直方图;

(II)估计该校学生身高在 的概率;
的概率;
(III)从样本中身高在180 190cm之间的男生中任选2人,求至少有1人身高在185
190cm之间的男生中任选2人,求至少有1人身高在185 190cm之间的概率。
190cm之间的概率。
【解析】第一问样本中男生人数为40 ,
由分层抽样比例为10%可得全校男生人数为400
(2)中由表1、表2知,样本中身高在 的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在 的频率
的频率
故由 估计该校学生身高在
估计该校学生身高在 的概率
的概率
(3)中样本中身高在180 185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185
185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185 190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图,故从样本中身高在180
190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图,故从样本中身高在180 190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185
190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185 190cm之间的可能结果数为9,因此,所求概率
190cm之间的可能结果数为9,因此,所求概率
由表1、表2知,样本中身高在 的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的学生人数为:5+14+13+6+3+1=42,样本容量为70 ,所以样本中学生身高在
的频率
 -----------------------------------------6分
-----------------------------------------6分
故由 估计该校学生身高在
估计该校学生身高在 的概率
的概率 .--------------------8分
.--------------------8分
(3)样本中身高在180 185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185
185cm之间的男生有4人,设其编号为①②③④ 样本中身高在185 190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:
190cm之间的男生有2人,设其编号为⑤⑥从上述6人中任取2人的树状图为:

--10分
故从样本中身高在180 190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185
190cm之间的男生中任选2人得所有可能结果数为15,求至少有1人身高在185 190cm之间的可能结果数为9,因此,所求概率
190cm之间的可能结果数为9,因此,所求概率
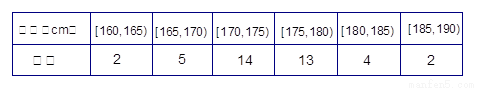
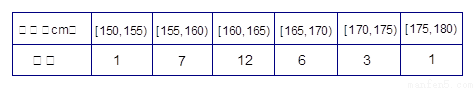

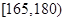 的概率;
的概率;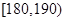 的男生中任选3人,设
的男生中任选3人,设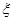 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在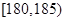 的人数,求
的人数,求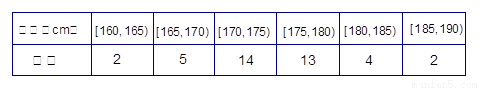 表1:男生身高频数分布表
表1:男生身高频数分布表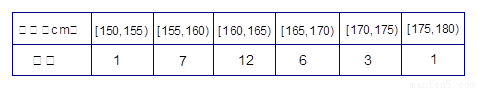 表2:女生身高频数分布表
表2:女生身高频数分布表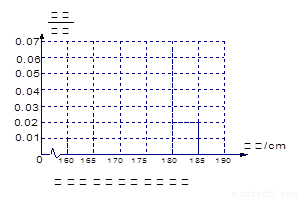
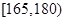 的概率;
的概率;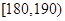 的男生中任选3人,设
的男生中任选3人,设 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在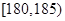 的人数,求
的人数,求 表1:男生身高频数分布表
表1:男生身高频数分布表 表2:女生身高频数分布表
表2:女生身高频数分布表 (1)求该校男生的人数并完成下面频率分布直方图;
(1)求该校男生的人数并完成下面频率分布直方图; 的概率;
的概率; 的男生中任选3人,设
的男生中任选3人,设 表示所选3人中身高(单位:cm)在
表示所选3人中身高(单位:cm)在 的人数,求
的人数,求